
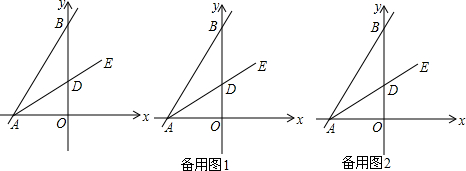
分析 (1)在Rt△AOD中,由勾股定理得:AD=4$\sqrt{3}$,从而可求得OB=6$\sqrt{3}$,故此可求得点B的坐标;
(2)当0<t<2$\sqrt{3}$时,PD=AD-AP;当t≥2$\sqrt{3}$时,PD=PA-AD;
(3)先求得点F的坐标,然后求得直线AD的解析式,列出设出点P的坐标,最后分为PF=DF、DF=DP,PF=PD三种情况,依据两点之间的距离公式列方程求解即可.
解答 解:(1)在Rt△AOD中,由勾股定理得:AD=$\sqrt{A{O}^{2}+O{D}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.
∵AD=BD,
∴BD=4$\sqrt{3}$.
∴OB=OD+BD=2$\sqrt{3}$+4$\sqrt{3}$=6$\sqrt{3}$.
∴点B的坐标为(0,6$\sqrt{3}$).
(2)当0<t<2$\sqrt{3}$时,PD=AD-AP=4$\sqrt{3}$-2t;
当t≥2$\sqrt{3}$时,PD=PA-AD=2t-4$\sqrt{3}$.
∴d与t的函数关系式为d=$\left\{\begin{array}{l}{4\sqrt{3}-2t(0<t<2\sqrt{3})}\\{2t-4\sqrt{3}(t≥2\sqrt{3})}\end{array}\right.$.
(3)设AB的解析式为y=kx+b,将点A、点B的坐标代入解析式得:$\left\{\begin{array}{l}{-6k+b=0}\\{b=6\sqrt{3}}\end{array}\right.$,
解得:k=$\sqrt{3}$,b=6$\sqrt{3}$.
∴直线AB的解析式为y=$\sqrt{3}x$+6$\sqrt{3}$.
将y=2$\sqrt{3}$代入得:$\sqrt{3}x+6\sqrt{3}$=2$\sqrt{3}$.
解得:x=-4.
∴点F的坐标为(-4,2$\sqrt{3}$).
设直线AD的解析式为y1=k1x+b1.
将点A和点D的坐标代入得:$\left\{\begin{array}{l}{{-6k}_{1}+{b}_{1}=0}\\{{b}_{1}=2\sqrt{3}}\end{array}\right.$.
解得:k1=$\frac{\sqrt{3}}{3}$,b1=2$\sqrt{3}$.
∴AD的解析式为y1=$\frac{\sqrt{3}}{3}x+2\sqrt{3}$.
设当运动时间为t秒时,点P的坐标为(-6+$\sqrt{3}t$,t).
当PF=DF时,由两点之间的距离公式得:$(-6+\sqrt{3}t+4)^{2}+(t-2\sqrt{3})^{2}$=42.
解得:${t}_{1}=2\sqrt{3}$,t2=0(舍去).
当DF=DP时,$(-6+\sqrt{3}t)^{2}+(2\sqrt{3}-t)^{2}$=42.
解得:${t}_{1}=2\sqrt{3}+2\sqrt{5}$,${t}_{2}=2\sqrt{3}-2\sqrt{5}$(舍去).
当PF=PD时,$(-6+\sqrt{3}t+4)^{2}+(t-2\sqrt{3})^{2}$=$(-6+\sqrt{3}t)^{2}+(t-2\sqrt{3})^{2}$.
解得:t=$\frac{4\sqrt{3}}{3}$.
综上所述,当t=2$\sqrt{3}$,或t=2$\sqrt{3}$+2$\sqrt{5}$,或t=$\frac{4\sqrt{3}}{3}$时,△DFP为等腰三角形.
点评 本题主要考查的是一次函数的综合应用、勾股定理的应用、待定系数法求一次函数的解析式、两点间的距离公式的应用,分类讨论是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正六边形的一个内角是108° | |
| B. | 不可能事件发生的概率为1 | |
| C. | 不在同一直线上的三个点确定一个圆 | |
| D. | 两边及其一边的对角线相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
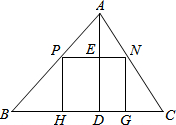 如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com