
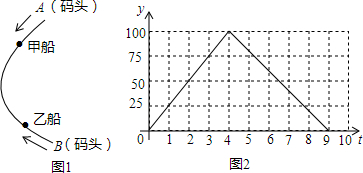
分析 (1)由函数图象的数据,根据行程问题的数量关系就可以求出结论;
(2)当0≤t≤2时,设y乙与时间t之间的函数关系式为y乙=kx+b;当2<t≤4时,设y乙与时间t之间的函数关系式为y乙=k1x+b1;由待定系数法就可以求出结论;
(3)通过描点法画出函数图象即可.
解答 解:(1)甲船顺流航行的速度:100÷4=25(km/h),逆流航行的速度:100÷(9-4)=20(km/h);
故答案为:25,20;
(2)当0≤t≤5时,设y乙与时间t之间的函数关系式为y乙=kx+b,由题意,得
$\left\{\begin{array}{l}{b=100}\\{5k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-20}\\{b=100}\end{array}\right.$
∴y乙=-20t+100
当5<t≤9时,设y乙与时间t之间的函数关系式为y乙=k1x+b1,由题意,得
$\left\{\begin{array}{l}{5{k}_{1}+{b}_{1}=0}\\{9{k}_{1}+{b}_{1}=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=25}\\{{b}_{1}=-125}\end{array}\right.$,
∴y乙=25t-125.
(3)如图2所示;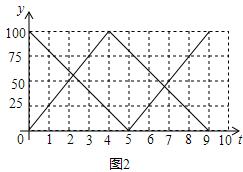
点评 本题考查了行程问题的数量关系时间=路程÷速度的运用,一次函数的图象的运用,待定系数法求一次函数的解析式的运用,列表发画函数图象的运用,解答时求出函数的解析式是关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
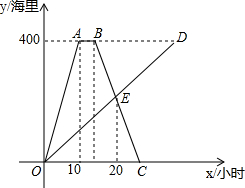 巡洋舰完成某海域巡航任务返回基地补给,同时海警船前往相同海域执怯(巡洋舰与海警船始终在同一航线上航行),巡洋舰返回基地修整5小时后立即按原路原速返回,如图是巡洋舰与海警船离各自出发地的路程y(单位:海里)与海警船航行时间x(单位:时)的承数图象.
巡洋舰完成某海域巡航任务返回基地补给,同时海警船前往相同海域执怯(巡洋舰与海警船始终在同一航线上航行),巡洋舰返回基地修整5小时后立即按原路原速返回,如图是巡洋舰与海警船离各自出发地的路程y(单位:海里)与海警船航行时间x(单位:时)的承数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
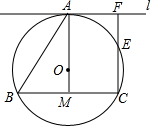 过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,
过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
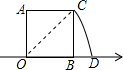 如图,以数轴的单位长线段为边作一个正方形AOBC,以数轴的原点圆心,对角线OC为半径画弧,交数轴于点D,则点D表示的数是$\sqrt{2}$.
如图,以数轴的单位长线段为边作一个正方形AOBC,以数轴的原点圆心,对角线OC为半径画弧,交数轴于点D,则点D表示的数是$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
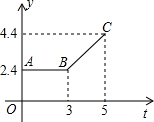 如图所示的折线ABC表示从甲地到乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象,通话时间不足一分钟按一分钟计费.
如图所示的折线ABC表示从甲地到乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象,通话时间不足一分钟按一分钟计费.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com