分析:(1)根据方差的定义的公式展开,进行整理得出命题的正确性;
(2)结合方差s
2=
[x
2+(y-1)
2+(x-y)
2]-(
)
2=
-(-
)
2,当且仅当-x=y-1=x-y=
=-
时,求出即可.
解答:解:(1)∵
s2=[(x1-)2+(x2-)2+…+(xn-)2],
=
[x
12+
() 2-2x
1+x
22+
() 2-2
x2+…+x
n2+
() 2-2x
n],
=
(x
12+x
22+…+x
n2)+
(
() 2+
() 2+…+
() 2)+
(-2x
1-2
x2-…-2x
n],
=
(x
12+x
22+…+x
n2)+
() 2+
(-2x
1-2
x2-…-2x
n],
=
(x
12+x
22+…+x
n2)+
() 2-2
(x
1+x
2+…+x
n],
=
(x
12+x
22+…+x
n2)-
() 2,
∴
s2=(++…+)- 2;
当x
1=x
2=…=x
n=
时,
s
2=
() 2-
() 2=0,
∴此时方差s
2取最小值0;
(2)设数据-x,(y-1),x-y的平均数为:
=
[(-x)+(y-1)+(x-y)],
=-
,
方差s
2=
[x
2+(y-1)
2+(x-y)
2]-(
)
2=
-(-
)
2,
当且仅当-x=y-1=x-y=
=-
时,
s
2=0,
此时x=
,y=
.
点评:此题主要考查了方差公式的证明以及综合应用,正确的将公式变形是解决问题的关键.



 ,方差
,方差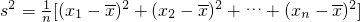 .
.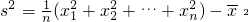 ;并且s2≥0,当x1=x2=…=xn=
;并且s2≥0,当x1=x2=…=xn= 时,方差s2取最小值0;
时,方差s2取最小值0;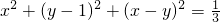 的一切实数对(x,y).
的一切实数对(x,y). ,方差
,方差 .
. ;并且s2≥0,当x1=x2=…=xn=
;并且s2≥0,当x1=x2=…=xn=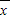 时,方差s2取最小值0;
时,方差s2取最小值0; 的一切实数对(x,y).
的一切实数对(x,y).