
【题目】如图,矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.

科目:初中数学 来源: 题型:
【题目】如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
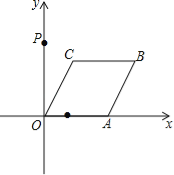
(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
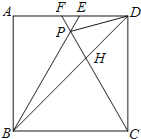
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②![]() =
=![]() ;③DP2=PHPB;④tan∠DBE=2﹣
;③DP2=PHPB;④tan∠DBE=2﹣![]() .
.
其中正确的是( )
A.①②③④ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
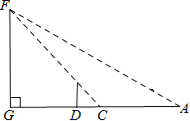
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
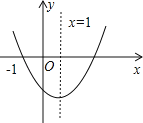
A.ac<0
B.b<0
C.b2﹣4ac<0
D.x=3关于x方程ax2+bx+c=0一个根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列能判定三角形是等腰三角形的是( )
A. 有两个角为30°、60°
B. 有两个角为40°、80°
C. 有两个角为50°、80°
D. 有两个角为100°、120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com