
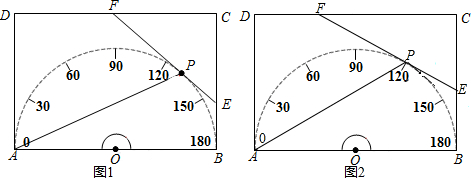
分析 (1)由∠AOP=136°可求出∠POB,进而求出∠PAB,用同样的方法就可求出α与n的关系.
(2)利用(1)中的α与n的关系式得到∠PAB=30°,所以通过解直角△APB即可得到弦AP的长度.
(3)运用切线长定理即可解决问题.
解答 解:(1)连接OP,如图1,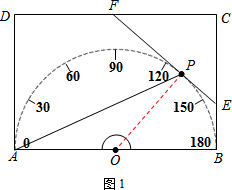
由题可知:∠AOP=136°.
∴∠POB=44°.
∴∠PAB=22°.
∵∠AOP=n°,
∴∠POB=180°-n°.
∴∠PAB=α=$\frac{1}{2}$∠POB=$\frac{1}{2}$(180°-n°)=90°-$\frac{1}{2}$n°.
α与n的关系式α=90°-$\frac{1}{2}$n°.
故答案为:22°;
(2)如图2,连接PB.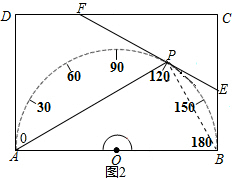
∵AB是直径,
∴∠APB=90°.
由(1)知,α=90°-$\frac{1}{2}$n°.
则当n=120时,α=30°,
∵AB=4,
∴AP=AB•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
(3)EB=EP.
理由如下:
如图1,∵四边形ABCD是矩形,
∴∠ABC=90°.
∴EB与半圆O相切.
又∵EP与半圆O相切,
∴由切线长定理得:EB=EP.
点评 此题属于圆的综合题,涉及了切线的性质,圆周角定理,切线长定理,三角函数值的知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
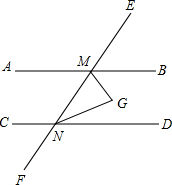 如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,试说明MG与NG的位置关系?
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,试说明MG与NG的位置关系?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
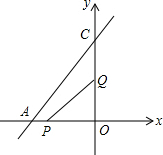 如图已知直线AC的函数解析式为y=$\frac{4}{3}$x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?
如图已知直线AC的函数解析式为y=$\frac{4}{3}$x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
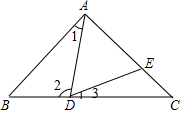 已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.
已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com