
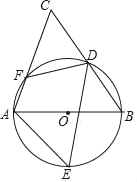
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)求证:∠E=∠C;
(2)若DF=6cm,cosB=![]() ,E是弧AB的中点,求DE的长.
,E是弧AB的中点,求DE的长.
【答案】(1)证明见解析;(2)DE= 14![]() .
.
【解析】分析:(1)直接利用圆周角定理得出AD⊥BC,再利用线段垂直平分线的性质得出AB=AC,即可得出∠E=∠C;
(2)根据cosB=![]() ,得出AB的长,即可求出AE的长,解直角三角形即可得到结论.
,得出AB的长,即可求出AE的长,解直角三角形即可得到结论.
详解:(1)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=12,
∵cosB=![]() ,
,
∴AB=20,
∵E是![]() 的中点,AB是⊙O的直径,
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=10,
∴AE=10![]() ,
,
∵E是![]() 的中点,
的中点,
∴∠ADE=∠BDE=45°,
∴DG=AG=ADsin45°=16×![]() =8
=8![]() ,EG=
,EG=![]() =6
=6![]() ,
,
∴DE=DG+GE=14![]() .
.



科目:初中数学 来源: 题型:
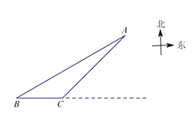
【题目】如图,海中有一个小岛 A,该岛四周 11 海里范围内有暗礁.有一货轮在海面上由西向正东方向航行,到达B处时它在小岛南偏西60°的方向上,再往正东方向行驶10海里后恰好到达小岛南偏西45°方向上的点C处.问:如果货轮继续向正东方向航行,是否会有触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) (-3)+(-8)-(-6)-7;
(2)-30×(![]() -
-![]() +
+![]() );
);
(3) (![]() -
-![]() )÷(-
)÷(-![]() )2-23;
)2-23;
(4)-42÷![]() -0.25×[5-(-3)2].
-0.25×[5-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
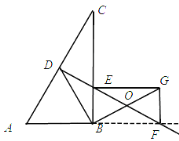
【题目】如图,在△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,点O是EF中点,连结BO井延长到G,且GO=BO,连接EG,FG
(1)试求四边形EBFG的形状,说明理由;
(2)求证:BD⊥BG
(3)当AB=BE=1时,求EF的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
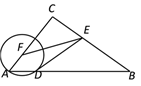
【题目】如图,Rt△ABC中,∠C=90°,AB=4![]() ,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )
,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )
A. 3![]() B. 2
B. 2![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
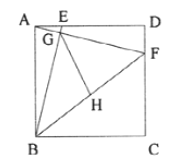
【题目】已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
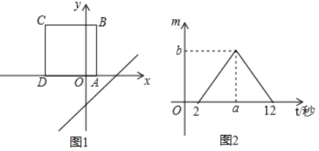
【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
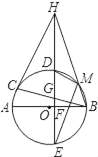
【题目】如图,AB,BC分别是⊙O的直径和弦,点D为![]() 上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD,ME.
上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD,ME.
求证:
(1)DE⊥AB;
(2)∠HMD=∠MHE+∠MEH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com