练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如图，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A对应，则角α的大小为（　　）
    A．30°B．60°C．90°D．120°

    分析 根据题意确定旋转中心后即可确定旋转角的大小．

    解答 解：如图：

    显然，旋转角为90°，
    故选C．

    点评 考查了旋转的性质，解题的关键是能够根据题意确定旋转中心的知识，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．直线y=kx（k＞0）与双曲线y=$\frac{6}{x}$交于A（x1，y1）和B（x2，y2）两点，则3x1y2-9x2y1的值为36．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列图形中是轴对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列图案

    其中，中心对称图形是（　　）
    A．①②B．②③C．②④D．③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．某服装店用10000元购进一批某品牌夏季衬衫若干件，很快售完；该店又用14700元钱购进第二批这种衬衫，所进件数比第一批多40%，每件衬衫的进价比第一批每件衬衫的进价多10元，求第一批购进多少件衬衫？设第一批购进x件衬衫，则所列方程为（　　）
    A．$\frac{10000}{x}$-10=$\frac{14700}{（1+40%）x}$B．$\frac{10000}{x}$+10=$\frac{14700}{（1+40%）x}$
    C．$\frac{10000}{（1-40%）x}$-10=$\frac{14700}{x}$D．$\frac{10000}{（1-40%）x}$+10=$\frac{14700}{x}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

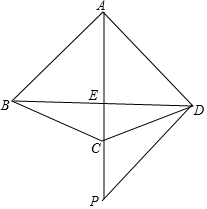    2．如图，四边形ABCD中，AB=AC=AD，AC平分∠BAD，点P是AC延长线上一点，且PD⊥AD．
    （1）证明：∠BDC=∠PDC；
    （2）若AC与BD相交于点E，AB=1，CE：CP=2：3，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

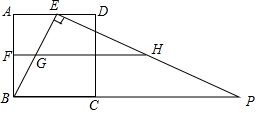    6．如图，正方形ABCD的边长为4，点E、F分别是边AD、AB的中点，点P是BC延长线上一点，且EP⊥EB，过点F作FH∥BP，分别交EB、EP于G、H两点，将△EGH绕点E逆时针旋转α（0°＜α＜90°），得到△EMN（M、N分别是G、H的对应点），使直线MN恰好经过点B．
    （1）求BP的长；
    （2）△EBM与△EPN相似吗？说明理由；
    （3）求旋转角α的大小．（只耍求出α的某一个三角函数值即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

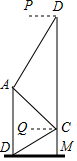    3．如图，某中学在教学楼前新建了一座雕塑AB，为了测量雕塑的高度，小明在二楼找到一点C，利用三角尺测得雕塑顶端点A的仰角∠QCA为45°，底部点B的俯角∠QCB为30°，小华在五楼找到一点D，利用三角尺测得点A的俯角∠PDA为60°，若AD为8m，则雕塑AB的高度为多少？（结果精确到0.1m，参考数据：$\sqrt{3}$≈1.73）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

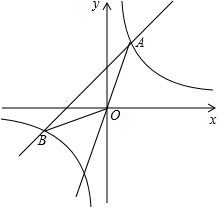    4．如图，直线y=4x与反比例函数y=$\frac{k}{x}$（k≠0）相交与点A（1，a），B是反比例函数图象上一点，直线OB与x轴的夹角为α，且tanα=$\frac{1}{4}$．
    （1）求k的值．
    （2）求点B的坐标．
    （3）设点P点在y轴上，若△PAB是以AB为直角边的直角三角形，则点P的坐标为：（0，5）或（0，-5）．

    查看答案和解析>>

    同步练习册答案