
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
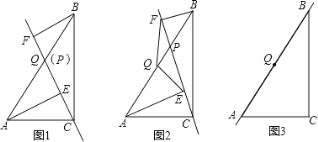
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
【答案】解:(1)AE∥BF,QE=QF。
(2)QE=QF,证明如下:
如图,延长FQ交AE于D,
![]()
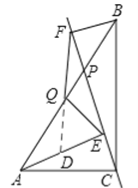
∵AE∥BF,∴∠QAD=∠FBQ。
在△FBQ和△DAQ中,∵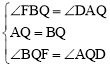 ,
,
∴△FBQ≌△DAQ(ASA)。∴QF=QD。
∵AE⊥CP,∴EQ是直角三角形DEF斜边上的中线。
∴QE=QF=QD,即QE=QF。
(3)(2)中的结论仍然成立。证明如下:
如图,延长EQ、FB交于D,
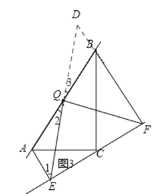
∵AE∥BF,∴∠1=∠D。
在△AQE和△BQD中,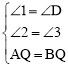 ,
,
∴△AQE≌△BQD(AAS),∴QE=QD。
∵BF⊥CP,∴FQ是斜边DE上的中线。∴QE=QF。
【解析】(1)证△BFQ≌△AEQ即可。理由是:
如图,∵Q为AB中点,∴AQ=BQ。
∵BF⊥CP,AE⊥CP,∴BF∥AE,∠BFQ=∠AEQ。
在△BFQ和△AEQ中,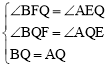 ,∴△BFQ≌△AEQ(AAS)。∴QE=QF。
,∴△BFQ≌△AEQ(AAS)。∴QE=QF。
(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可。
(3)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可。


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
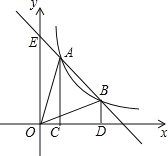
【题目】如图,已知A(a,m)、B(2a,n)是反比例函数y=![]() (k>0)与一次函数y=-
(k>0)与一次函数y=-![]() x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现用a根长度相同的火柴棒,按如图①摆放时可摆成m个正方形,按如图②摆放时可摆放2n个正方形.

(1)如图①,当m=2时,a= ,如图②,当n=3时,a= ;
(2) m与n之间有何数量关系,请你写出来并说明理由;
(3)现有56根火柴棒,现用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状。请你直接写出一种摆放方法,并通过计算验证你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
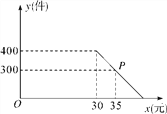
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3y2-2y+4y2;
(2)![]() +4-3st-4;
+4-3st-4;
(3)2(2ab+3a)-3(2a-ab);
(4)a2-[-4ab+(ab-a2)]-2ab.
(5).(-1)3-![]() ÷3×[3-(-3)2];
÷3×[3-(-3)2];
(6)![]() ×
×![]() ÷(-9+19);
÷(-9+19);
(7)-24×![]() ;
;
(8)(-81)÷![]() +
+![]() ÷(-16);
÷(-16);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天的生产量与计划量相比有出入。下表是某周的生产情况(超产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +4 | -2 | -5 | +13 | -11 | +17 | -9 |
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖6元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
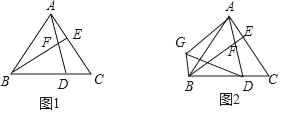
【题目】如图1,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=AE,AD与BE相交于点F.
(1)求证:∠ABE=∠CAD;
(2)如图2,以AD为边向左作等边△ADG,连接BG.
ⅰ)试判断四边形AGBE的形状,并说明理由;
ⅱ)若设BD=1,DC=k(0<k<1),求四边形AGBE与△ABC的周长比(用含k的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com