
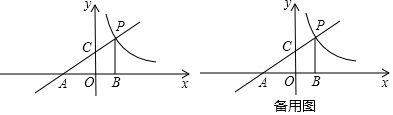
·ÖĪö £Ø1£©ĄūÓĆ“ż¶ØĻµŹż·ØæÉŅŌĒó³öµćA”¢CµÄ×ų±ź£¬ÓÉ”÷ACO”×”÷APB£¬ĶĘ³ö$\frac{OA}{AB}$=$\frac{OC}{PB}$=$\frac{2}{3}$£¬ĶĘ³öOB=2£¬PB=3£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
£Ø2£©ČēĶ¼1ÖŠ£¬×÷µćP¹ŲÓŚxÖįµÄ¶Ō³ĘµćP”䣬Į¬½ÓQP”äÓėxÖį½»ÓŚµćM£¬LJ PM£¬“ĖŹ±PM+MQµÄÖµ×īŠ”£®Ēó³öÖ±ĻßP”äQµÄ½āĪöŹ½¼“æÉ£®
£Ø3£©ÉčRµćµÄ×ų±źĪŖ£Øm£¬$\frac{6}{m}$£©£¬·ÖĮ½ÖÖĒéŠĪ·Ö±šĄūÓĆĻąĖĘČż½ĒŠĪµÄŠŌÖŹ£¬ĮŠ³ö·½³Ģ½ā¾öĪŹĢā£®
½ā“š ½ā£ŗ£Ø1£©”ßÖ±Ļßy=$\frac{1}{2}$x+2·Ö±š½»x”¢yÖįÓŚµćA”¢C£¬
”ąAµć×ų±ź£Ø-4£¬0£©£¬Cµć×ų±ź£Ø0£¬2£©£¬
”ßS”÷AOC=$\frac{1}{2}$”Į4”Į2=4£¬
”ßOC”ĪPB£¬S”÷ABP=9£¬
”ą”÷ACO”×”÷APB£¬
”ą$\frac{OA}{AB}$=$\frac{OC}{PB}$=$\frac{2}{3}$£¬
”ąAB=6£¬PB=3£¬
”ąOB=2£¬
”ąP£Ø2£¬3£©
¹Ź“š°øĪŖ£Ø-4£¬0£©£¬£Ø0£¬2£©£¬£Ø2£¬3£©£®
£Ø2£©ČēĶ¼1ÖŠ£¬×÷µćP¹ŲÓŚxÖįµÄ¶Ō³ĘµćP”䣬Į¬½ÓQP”äÓėxÖį½»ÓŚµćM£¬LJ PM£¬“ĖŹ±PM+MQµÄÖµ×īŠ”£®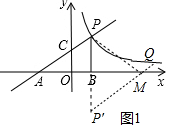
”ßµćP£Ø2£¬3£©ŌŚ£¬·“±ČĄżŗÆŹży=$\frac{k}{x}$ÉĻ£¬
”ąk=6£¬
”ąQ£Ø6£¬1£©£¬P”ä£Ø2£¬-3£©£¬
”ąÖ±ĻßP”äQŹĒ½āĪöŹ½ĪŖy=x-5£¬
Įīy=0£¬µĆx=5£¬
”ąM£Ø5£¬0£©£®
£Ø3£©ČēĶ¼2ÖŠ£¬ÉčRµćµÄ×ų±źĪŖ£Øm£¬$\frac{6}{m}$£©£¬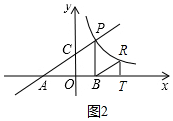
”ßPµć×ų±źĪŖ£Ø2£¬3£©£¬
Ó֔ߔ÷BRT”×”÷ACO£¬
”ą$\frac{OA}{BT}$=$\frac{CO}{RT}$£¬
”ą$\frac{4}{m-2}$=$\frac{2}{\frac{6}{m}}$£¬
½āµĆm1=1+$\sqrt{13}$£¬m2=1-$\sqrt{13}$£ØÉįČ„£©£¬
”ąR£Ø1+$\sqrt{13}$£¬$\frac{\sqrt{13}-1}{2}$£©£¬
¢ŚČēĶ¼3ÖŠ£¬”÷BRT”×”÷CAOŹ±£¬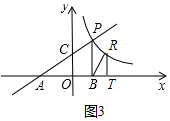
”ą$\frac{OA}{RT}$=$\frac{OC}{BT}$Ź±£¬
”ą$\frac{4}{\frac{6}{m}}$=$\frac{2}{m-2}$£¬
½āµĆm1=3£¬m2=-1£ØÉįČ„£©
”ąR£Ø3£¬2£©
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄµćR×ų±źĪŖ£Ø1+$\sqrt{13}$£¬$\frac{\sqrt{13}-1}{2}$£©»ņ£Ø3£¬2£©£®
µćĘĄ ±¾Ģā漲鷓±ČĄżŗÆŹż×ŪŗĻĢā”¢ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢Öį¶Ō³Ę-×ī¶ĢĪŹĢāµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶£¬Ń§»įĄūÓĆ²ĪŹż½ā¾öĪŹĢā£¬Ń§»įÓĆ·½³ĢµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£¬ŹōÓŚÖŠæ¼³£æ¼ĢāŠĶ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
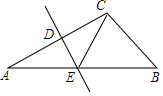 ČēĶ¼£¬”÷ABCÖŠ£¬AB=10£¬BC=6£¬±ßACµÄ“¹Ö±Ę½·ÖĻß·Ö±š½»AB”¢ACÓŚµćE”¢D£¬Ōņ”÷BCEµÄÖܳ¤ĪŖ16£®
ČēĶ¼£¬”÷ABCÖŠ£¬AB=10£¬BC=6£¬±ßACµÄ“¹Ö±Ę½·ÖĻß·Ö±š½»AB”¢ACÓŚµćE”¢D£¬Ōņ”÷BCEµÄÖܳ¤ĪŖ16£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬PBĪŖ”ŃOµÄĒŠĻߣ¬BĪŖĒŠµć£¬Ö±ĻßPO½»”ŃOÓŚµćE£¬F£¬¹żµćB×÷POµÄ“¹ĻßBA£¬“¹×ćĪŖµćD£¬½»”ŃOÓŚµćA£¬ŃÓ³¤AOÓė”ŃO½»ÓŚµćC£¬Į¬½ÓBC£¬AF£®
ČēĶ¼£¬PBĪŖ”ŃOµÄĒŠĻߣ¬BĪŖĒŠµć£¬Ö±ĻßPO½»”ŃOÓŚµćE£¬F£¬¹żµćB×÷POµÄ“¹ĻßBA£¬“¹×ćĪŖµćD£¬½»”ŃOÓŚµćA£¬ŃÓ³¤AOÓė”ŃO½»ÓŚµćC£¬Į¬½ÓBC£¬AF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ČĪŅāĀņŅ»ÕŵēӰʱ£¬×łĪ»ŗÅŹĒżŹż | |
| B£® | “üÖŠÖ»ÓŠ5Ö»»ĘĒņ£¬Ćž³öŅ»øöĒņŹĒ°×Ēņ | |
| C£® | ÓĆ³¤¶Č·Ö±šŹĒ2cm£¬3cm£¬6cmµÄĻøľĢõŹ×Ī²ĻąĮ¬×é³ÉŅ»øöČż½ĒŠĪ | |
| D£® | “Ó·Ö±šŠ“ÓŠ2£¬4£¬6µÄČżÕÅæØʬ֊Ė껜³é³öŅ»ÕÅ£¬æØʬÉĻµÄŹż×ÖÄܱ»2Õū³ż |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 Ķ¼£Ø1£©ŹĒŅ»øö³¤ĪŖ 2a£¬æķĪŖ2b£Øa£¾b£©µÄ³¤·½ŠĪ£¬ÓĆ¼ōµ¶ŃŲĶ¼ÖŠŠéĻߣضŌ³ĘÖį£©¼ōæŖ£¬°ŃĖü·Ö³ÉĖÄæéŠĪדŗĶ“󊔶¼Ņ»ŃłµÄŠ”³¤·½ŠĪ£¬Č»ŗó°“Ķ¼£Ø2£©ÄĒѳʓ³ÉŅ»øöÕż·½ŠĪ£¬ŌņÖŠ¼äæյIJæ·ÖµÄĆ껿ŹĒ£Ø””””£©
Ķ¼£Ø1£©ŹĒŅ»øö³¤ĪŖ 2a£¬æķĪŖ2b£Øa£¾b£©µÄ³¤·½ŠĪ£¬ÓĆ¼ōµ¶ŃŲĶ¼ÖŠŠéĻߣضŌ³ĘÖį£©¼ōæŖ£¬°ŃĖü·Ö³ÉĖÄæéŠĪדŗĶ“󊔶¼Ņ»ŃłµÄŠ”³¤·½ŠĪ£¬Č»ŗó°“Ķ¼£Ø2£©ÄĒѳʓ³ÉŅ»øöÕż·½ŠĪ£¬ŌņÖŠ¼äæյIJæ·ÖµÄĆ껿ŹĒ£Ø””””£©| A£® | a2-b2 | B£® | £Øa-b£©2 | C£® | £Øa+b£©2 | D£® | ab |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com