
 分别表示三种不同物体,用天平比较他们质量的大小,两种情况如图4所示,则每个
分别表示三种不同物体,用天平比较他们质量的大小,两种情况如图4所示,则每个 ”按质量从小到大的顺序为( )
”按质量从小到大的顺序为( )
科目:初中数学 来源: 题型:阅读理解
 似比(a:b).
似比(a:b).| S甲 |
| S乙 |
| 6a2 |
| 6b2 |
| a |
| b |
| V甲 |
| V乙 |
| a3 |
| b3 |
| a |
| b |
 常相似,现有大小两种不同的价钱,如下图所示,鱼长10厘米的每条10元,鱼长13厘米的每条15元.康子不知道买哪种更好些,你能否帮他出出主意.
常相似,现有大小两种不同的价钱,如下图所示,鱼长10厘米的每条10元,鱼长13厘米的每条15元.康子不知道买哪种更好些,你能否帮他出出主意.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
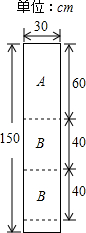 (2013•本溪三模)某公司装修需要A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型,B型板材,共有下列三种裁法,每种裁法所需费用如表所示:(如图是裁法一的裁剪示意图)
(2013•本溪三模)某公司装修需要A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型,B型板材,共有下列三种裁法,每种裁法所需费用如表所示:(如图是裁法一的裁剪示意图)| 裁法一 | 裁法二 | 裁法三 | |
| A型板材块数 | 1 | 2 | 0 |
| B型板材块数 | 2 | m | n |
| 费用(元/张) | 50 | 20 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某工厂生产的边长为1米的正方形装饰材料ABCD如图所示,点E在BC上,点F是CD的中点.△ABE、△CEF和四边形AEFD分别由Ⅰ型、Ⅱ型、Ⅲ型三种材料制成.
某工厂生产的边长为1米的正方形装饰材料ABCD如图所示,点E在BC上,点F是CD的中点.△ABE、△CEF和四边形AEFD分别由Ⅰ型、Ⅱ型、Ⅲ型三种材料制成.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
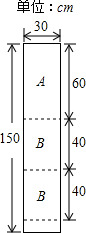 某公司装修需要A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型,B型板材,共有下列三种裁法,每种裁法所需费用如表所示:(如图是裁法一的裁剪示意图)
某公司装修需要A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型,B型板材,共有下列三种裁法,每种裁法所需费用如表所示:(如图是裁法一的裁剪示意图)| 裁法一 | 裁法二 | 裁法三 | |
| A型板材块数 | 1 | 2 | 0 |
| B型板材块数 | 2 | m | n |
| 费用(元/张) | 50 | 20 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com