
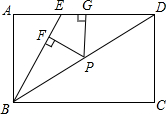
 如图,E是矩形ABCD边AD上的一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE于F,PG⊥AD与G,请你猜想PF、PG、AB它们之间有什么关系?并证明你的结论.
如图,E是矩形ABCD边AD上的一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE于F,PG⊥AD与G,请你猜想PF、PG、AB它们之间有什么关系?并证明你的结论. 分析 连接PE,把△BED分成△BEP和△DEP两个三角形,然后利用三角形的面积列式进行计算即可得证.
解答 答:PF+PG=AB,
证明:连接PE,
∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP
=$\frac{1}{2}$BE•PF+$\frac{1}{2}$ED•PG
=$\frac{1}{2}$ED•(PF+PG),
又∵四边形ABCD是矩形,
∴BA⊥AD,
∴S△BED=$\frac{1}{2}$ED•AB,
∴$\frac{1}{2}$ED•(PF+PG)=$\frac{1}{2}$ED•AB,
∴PF+PG=AB.
点评 本题考查了矩形的性质,三角形的面积,作辅助线,利用三角形的面积的两种表示方法证明更简单.


科目:初中数学 来源: 题型:解答题
 如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF.
如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{10x-10y=50}\\{2x+2y=50}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{10x+10y=50}\\{2x+2y=50}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{10y-10x=50}\\{2x+2y=50}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{10x-10y=50}\\{2x-2y=50}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,E是AB的中点.
如图,在梯形ABCD中,AD∥BC,E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com