解:(1)将A(1,0)、C(-2,4)代入直线y=mx+n得:
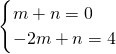
,
解得:
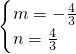
,
故直线解析式为:
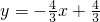
.
将A(1,0)代入抛物线
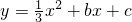
及对称轴为直线x=-2得:

,
解得:
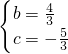
,
故抛物线解析式为:
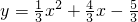
.
(2)存在.
如图1,图形简化为图2
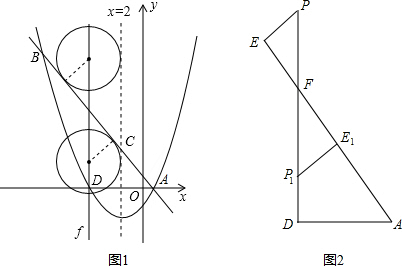
直线f解析式:x=-5,故圆半径R=3,且F(-5,8).
易得△PEF∽△ADF,△P
1E
1F≌△PEF,其中PE=P
1E
1=R=3,AD=6,FD=8,P
1F=PF.
在Rt△ADF中,由勾股定理得:AF=10,由
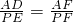
得:PF=5.
∴PD=13,P
1D=3.
∴
P(-5,13)、P
1(-5,3).
综上可得存在点P的坐标为(-5,13)或(-5,3).
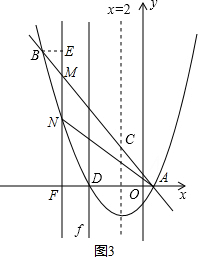
(3)如图3:
联立直线与抛物线解析式得:

,
解得交点B的坐标:(-9,

).
设点M(q,-

q+

),N(q,

q
2+

q-

),
所以:MN=(-

q+

)-(

q
2+

q-

)=-

q
2-

q+3=-

(q+4)
2+

.
S
△ABN=S
△AMN+S
△BMN=

MN•AF+

MN•BE=

MN(AF+BE)=5MN=-

(q+4)
2+
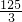
.
当q=-4时,S
△ABN有最大值
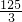
;此时:MN=

.
分析:(1)利用待定系数法可以求出直线y=mx+n的解析式;在解二次函数的解析式时,可由其对称轴方程求出b的值,再代入A点的坐标可以求出c的值.
(2)此题需要从图形入手,显然在直线AB的上下方各有一个符合条件的P点,那么可以将图形进行简化(如解答部分的图示),在简化的图形中,△P
1E
1F≌△PEF且△PEF∽△ADF;圆的半径可由直线f和直线x=-2的距离得出(即PE、P
1E
1的长),AD、FD的长不难得到,那么由相似三角形即可求出PF的长,进而能求出PD、P
1D的长,由此求出圆心的坐标.
(3)点B的坐标不难求出,根据直线AB和抛物线的解析式,可以先用一个未知数表达出点M、N的坐标,以MN为底,A、B点的横坐标差的绝对值为高(也可将△ABN分成两个三角形来分析),即可得到关于△ABN的面积和未知数的函数解析式,根据函数的性质求解即可.
点评:此题考查了函数解析式的确定、直线和圆的位置关系、相似三角形以及全等三角形的应用、三角形面积的求法等重要知识点;(2)题中,对图形进行简化能使得繁杂的题目更加直观;最后一题是二次函数综合题中考查频率比较大的一种类型题,需要牢固掌握.

 已知:如图,直线y=mx+n与抛物线
已知:如图,直线y=mx+n与抛物线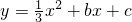 交于点A(1,0)和点B,与抛物线的对称轴x=-2交于点C(-2,4),直线f过抛物线与x轴的另一个交点D且与x轴垂直.
交于点A(1,0)和点B,与抛物线的对称轴x=-2交于点C(-2,4),直线f过抛物线与x轴的另一个交点D且与x轴垂直.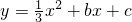 的解析式;
的解析式;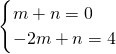 ,
,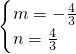 ,
,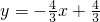 .
.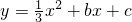 及对称轴为直线x=-2得:
及对称轴为直线x=-2得: ,
,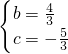 ,
,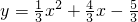 .
.
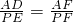 得:PF=5.
得:PF=5. P(-5,13)、P1(-5,3).
P(-5,13)、P1(-5,3). ,
, ).
). q+
q+ ),N(q,
),N(q, q2+
q2+ q-
q- ),
), q+
q+ )-(
)-( q2+
q2+ q-
q- )=-
)=- q2-
q2- q+3=-
q+3=- (q+4)2+
(q+4)2+ .
. MN•AF+
MN•AF+ MN•BE=
MN•BE= MN(AF+BE)=5MN=-
MN(AF+BE)=5MN=- (q+4)2+
(q+4)2+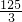 .
.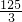 ;此时:MN=
;此时:MN= .
.

 阅读快车系列答案
阅读快车系列答案 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=