
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.

【答案】AE=BD,AE⊥BD
【解析】试题分析:由于条件可知CD=AC,BC=CE,且可求得∠ACE=∠DCB,所以△ACE≌△DCB,即AE=BD,∠CAE=∠CDB;又因为对顶角相∠AFC=∠DFH,所以∠DHF=∠ACD=90°,即AE⊥BD
试题解析:猜测AE=BD,AE⊥BD;
理由如下:
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
又∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB,(4分)
∵在△ACE与△DCB中,
AC=DC
∠ACE=∠DCB
EC=BC
∴△ACE≌△DCB(SAS),
∴AE=BD,(6分)∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD
故线段AE和BD的数量相等,位置是垂直关系


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
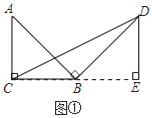
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
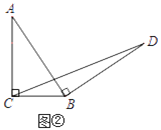
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
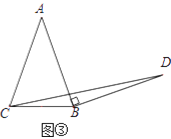
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,已知点O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )
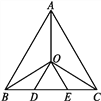
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB= ![]() ,则GE的长为
,则GE的长为 ![]() ,并简述求GE长的思路.
,并简述求GE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1 , 0),(x2 , 0),且x1<x2 , 图象上有一点M(x0 , y0)在x轴下方,对于以下说法: ①b2﹣4ac>0;
②x=x0是方程ax2+bx+c=y0的解;
③x1<x0<x2
④a(x0﹣x1)(x0﹣x2)<0;
⑤x0<x1或x0>x2 ,
其中正确的有( )
A.①②
B.①②④
C.①②⑤
D.①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)= ![]() .如:12=1×12=2×6=3×4,则F(12)=
.如:12=1×12=2×6=3×4,则F(12)= ![]() .则在以下结论:
.则在以下结论:
①F(5)=5;②F(24)= ![]() ;
;
③若a是一个完全平方数,则F(a)=1;
④若a是一个完全立方数,即a=x3(x是正整数),
则F(a)=x.则正确的结论有________(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com