
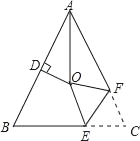
【题目】如图,△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
【答案】112.
【解析】
连接OB、OC,根据角平分线的定义求出∠BAO=28°,利用等腰三角形两底角相等求出∠ABC,根据线段垂直平分线上的点到两端点的距离相等可得OA=OB,再根据等边对等角求出∠OBA,然后求出∠OBC,再根据等腰三角形的性质可得OB=OC,然后求出∠OCE,根据翻折变换的性质可得OE=CE,然后利用等腰三角形两底角相等列式计算即可得解.
如图,连接OB、OC,

∵OA平分∠BAC,∠BAC=56°,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×56°=28°,
×56°=28°,
∵AB=AC,∠BAC=56°,
∴∠ABC=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() ×(180°﹣56°)=62°,
×(180°﹣56°)=62°,
∵OD垂直平分AB,
∴OA=OB,
∴∠OBA=∠BAO=28°,
∴∠OBC=∠ABC﹣∠OBA=62°﹣28°=34°,
由等腰三角形的性质,OB=OC,
∴∠OCE=∠OBC=34°,
∵∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠OEC=180°﹣2×34°=112°.
故答案是:112.


科目:初中数学 来源: 题型:
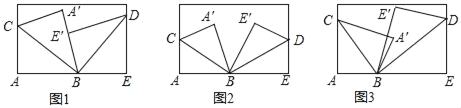
【题目】(1)将一张长方形纸片按如图1所示的方式折叠,BC、BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC、BD为折痕,若∠A′BE′=50°,求∠CBD的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC、BD为折痕,若∠A′BE′=α,请直接写出∠CBD的度数(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )
A.y3>y1>y2
B.y1>y3>y2
C.y3>y2>y1
D.y1>y2>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为 ![]() 。
。
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,直接写出∠ADB的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC , OD与AC交于点E.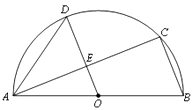
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2),

(1)请画出△ABC向左平移1个单位长度,再向上平移2个单位长度后的△A′B′C′,(其中A′、B′、C′分别是A、B、C的对应点)
(2)直接写出A′、B′、C′三点的坐标:A′(_____,______);B′(_____,______);C′(_____,______).
(3)△ABC的面积为______________平方单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com