
 如图,在四边形ABCD中,AB∥CD,∠A=90°,CD=2,AB=3,AD=7,点P为线段AD上一点,CP⊥BP,求DP的长.
如图,在四边形ABCD中,AB∥CD,∠A=90°,CD=2,AB=3,AD=7,点P为线段AD上一点,CP⊥BP,求DP的长. 分析 根据平行线的性质得到∠D=90°,由CP⊥BP,得到∠BPC=90°,于是得到∠DCP=∠APB,推出△PDC∽△BAP,得到比例式$\frac{CD}{AP}=\frac{PD}{AB}$,代入数据即可得到结论.
解答 解:∵AB∥CD,∠A=90°,
∴∠D=90°,
∵CP⊥BP,
∴∠BPC=90°,
∴∠DPC+∠APB=∠DPC+∠DCP=90°,
∴∠DCP=∠APB,
∴△PDC∽△BAP,
∴$\frac{CD}{AP}=\frac{PD}{AB}$,
即:$\frac{2}{7-PD}$=$\frac{PD}{3}$,
解得:PD=1或PD=6.
点评 本题考查了相似三角形的判定和性质,平行线的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
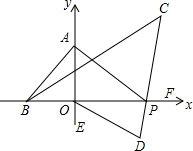 如图,在平面直角坐标系中,∠ABO=2∠BAO,P为x轴正半轴一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE
如图,在平面直角坐标系中,∠ABO=2∠BAO,P为x轴正半轴一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,以直线x=-1为对称轴的二次函数y=ax2+bx+c经过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a-2b+c>0;④若(-5,y1)($\frac{5}{2}$,y2)是该二次函数图象上的两个点,则y1>y2.其中说法正确的是①②④.(只填序号)
如图,以直线x=-1为对称轴的二次函数y=ax2+bx+c经过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a-2b+c>0;④若(-5,y1)($\frac{5}{2}$,y2)是该二次函数图象上的两个点,则y1>y2.其中说法正确的是①②④.(只填序号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 1883年,康托尔构造的这个分形,称作康托尔集,从数轴上单位长度线段开始,康托尔取走其中间三分之一而达到第一阶段,然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段,无限地重复这一过程,余下的无穷点集就称做康托尔集,上图是康托尔集的最初几个阶段,当达到第n个阶段时,余下的所有线段的长度之和为( )
1883年,康托尔构造的这个分形,称作康托尔集,从数轴上单位长度线段开始,康托尔取走其中间三分之一而达到第一阶段,然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段,无限地重复这一过程,余下的无穷点集就称做康托尔集,上图是康托尔集的最初几个阶段,当达到第n个阶段时,余下的所有线段的长度之和为( )| A. | $\frac{2n}{3}$ | B. | $\frac{2n}{3}$ | C. | ${(\frac{2}{3})^n}$ | D. | ${(\frac{2}{3})^{n-1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 观察下面的点阵图,探究其中的规律.摆第10个这样的“小屋子”需要59个点,写出摆第n个这样的“小屋子”需要的总点数,S与n的关系式6n-1.
观察下面的点阵图,探究其中的规律.摆第10个这样的“小屋子”需要59个点,写出摆第n个这样的“小屋子”需要的总点数,S与n的关系式6n-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com