
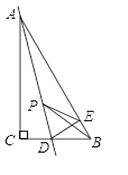
【题目】如图,在Rt△ABC中,∠C=Rt∠,∠ABC=60°,D是BC边上的点,CD=1,将△ACD沿直线AD翻折,点C恰好落在直线AB的边上的E处,若P是直线AD上的动点,则△PEB的周长最小值是____________ .
【答案】![]()
【解析】
根据折叠和等腰三角形性质得出,E关于AD的对称点为C,即当P和D重合时,PE+BP的值最小,即可此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,先求出BC和BE长,代入求出即可.
解:∵沿AD折叠C和E重合,
∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,
∴AD垂直平分CE,即C和E关于AD对称,CD=DE=1,
∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,
∵∠DEA=90°,
∴∠DEB=90°,
∵∠ABC=60°,DE=1,
∴BE=![]() ,BD=
,BD=![]() ,即BC=
,即BC=![]() ,
,
∴△PEB的周长的最小值是BC+BE=![]() +
+![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E,AD=8,AB=16.
(1)求证:DE=BE;
(2)求S△BEF;
(3)若M、N分别为线段CD、DB上的动点,直接写出(NC+NM)的最小值___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是直线x=﹣1.
(1)求m,n的值;
(2)x取什么值时,y随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
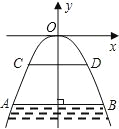
【题目】如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?
查看答案和解析>>
科目:初中数学 来源: 题型:
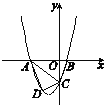
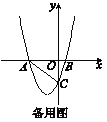
【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
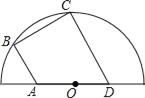
【题目】如图,四边形ABCD内接于半圆O,其中点A,D在直径上,点B,C在半圆弧上,AB∥CD,∠B=90°,若AO=3,∠BAD=120°,则BC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意,解答问题:
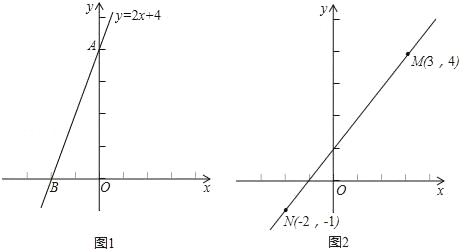
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com