
|
| p2-1 |
| 2 |
| p2+1 |
| 2 |
| p2-1 |
| 2 |


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
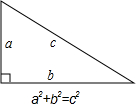 定理”.它揭示了一个直角三角形三条边之间的数量关系(如图).
定理”.它揭示了一个直角三角形三条边之间的数量关系(如图).| 12+12 |
| 2 |
| 12+22 |
| 5 |
| 10 |
| 10 |
| 13 |
| 13 |
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第8期 总第164期 华师大版 题型:044
下面是数学课堂上的一个学习片段,阅读后,请回答下面的问题
学习了勾股定理的有关内容后,张老师请同学们交流讨论这样一个问题:“已知Rt△ABC的两边长分别为3和4,请你求出第三边长的平方.”
同学们经片刻的思考与交流后,李明同学举手说:“第三边长的平方是25”;王华同学说:“第三边长的平方是7”.还有一些同学也提出了不同的看法
(1)假如你也在课堂上,你的意见如何?为什么?
(2)通过上面数学问题的讨论,你有什么感受?(用一句话表示)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com