
分析 如图,设AB与⊙O相切于点F,连接OF,OD,延长FO交CD于点E,首先证明OE⊥CD,在RT△EOD中,利用勾股定理即可解决问题.
解答 解:如图,设AB与⊙O相切于点F,连接OF,OD,延长FO交CD于点E.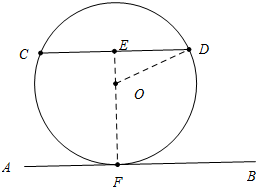
∵2πR=26π,
∴R=13,
∴OF=OD=13,
∵AB是⊙O切线,
∴OF⊥AB,
∵AB∥CD,
∴EF⊥CD即OE⊥CD,
∴CE=ED,
∵EF=18,OF=13,
∴OE=5,
在RT△OED中,∵∠OED=90°,OD=13,OE=5,
∴ED=$\sqrt{O{D}^{2}-O{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴CD=2ED=24.
故答案为24.
点评 本题考查切线的性质、垂径定理、勾股定理等知识,解题的关键是正确添加辅助线,利用垂径定理解决问题,属于中考常考题型.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:解答题
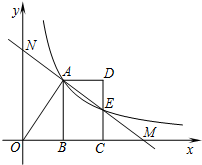 反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=$\frac{k}{x}$(x>0)的图象恰好经过DC的中点E.
反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=$\frac{k}{x}$(x>0)的图象恰好经过DC的中点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
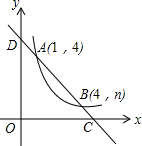 如图,直线y=ax+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
如图,直线y=ax+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
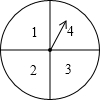 小明和小军两人一起做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于他们各自选择的数,就在做一次上述游戏,直至决出胜负.若小军事先选择的数是5,用列表或画树状图的方法求他获胜的概率.
小明和小军两人一起做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于他们各自选择的数,就在做一次上述游戏,直至决出胜负.若小军事先选择的数是5,用列表或画树状图的方法求他获胜的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
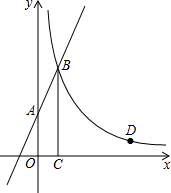 如图,直线y=2x+3与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
如图,直线y=2x+3与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com