
 ��2+A��2�����֡ߣ�x+
��2+A��2�����֡ߣ�x+ ��2��0����a��x+
��2��0����a��x+ ��2��0��ax2+bx+c=a��x+
��2��0��ax2+bx+c=a��x+ ��2+A��A����������x�����仯��y=ax2+bx+c��a��0��������ȡֵ�У���AΪ�������x=Bʱ��y��ֵ����A�����У���a��b��c��ʾ��A=
��2+A��A����������x�����仯��y=ax2+bx+c��a��0��������ȡֵ�У���AΪ�������x=Bʱ��y��ֵ����A�����У���a��b��c��ʾ��A= ______��B=______��
______��B=______�� ��B=-
��B=- ��
��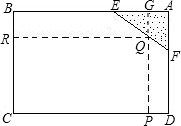
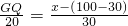 ��GQ=
��GQ=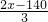 ��
��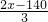 =
=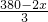 ��
��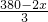
 x2+
x2+ x
x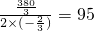 ʱ��y���=
ʱ��y���= ��6017
��6017


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| n(n-1) |
| 2 |
| ��ĸ��� | �����ɵ������εĸ��� | ||||
| 3 | 1 1 | ||||
| 4 | 4 4 | ||||
| 5 | 10 10 | ||||
| �� | �� | ||||
| n |
|
| n(n-1)(n-2) |
| 6 |
| n(n-1)(n-2) |
| 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��
��| ��ĸ��� | �����ɵ������εĸ��� |
| 3 | ________ |
| 4 | ________ |
| 5 | ________ |
| �� | �� |
| n | ________ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ĩ�� ���ͣ������
 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
�Ķ����в��ϣ���ɲ��Ϻ�����
�α����Ƶ�����������ȫƽ����ʽ�����������壬����ͼ�ε�������͡�
 ��ͼ1��һ���߳�Ϊ
��ͼ1��һ���߳�Ϊ![]() �������ο��Կ�����
�������ο��Կ�����
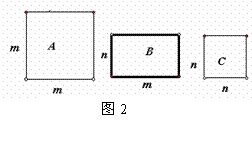 �߳�Ϊ
�߳�Ϊ![]() �������κͱ߳�Ϊ
�������κͱ߳�Ϊ![]() ���������Լ������ֱ�Ϊ
���������Լ������ֱ�Ϊ![]() �����������ι��ɡ�
�����������ι��ɡ�
���߳�Ϊ![]() �������ε�����������㷨��
�������ε�����������㷨��![]() �Լ�
�Լ�![]() ���ɴ˵õ���һ����ʽ��
���ɴ˵õ���һ����ʽ�� ![]() ���ɴ˷��ֿ������ü��ν��ʹ����еĹ�ʽ������ο��α���������ȵĽ���������⣺
���ɴ˷��ֿ������ü��ν��ʹ����еĹ�ʽ������ο��α���������ȵĽ���������⣺
�������ֲ�ͬ���͵ij����ε�ש������ͼ2��ʾ��������A��4�飬B��4�飬C��2�飬������Щ��ש�������Ϊ_______________________.��������еĵ�שҪƴ��һ�������Σ������1��___________�͵�ש����A��B,C���������ĵ�שƴ��Ҳ��ʾ��һ�������͵�ƽ���ļ������壬�����ú���![]() �ĵ�ʽд�����������ĺ͵�ƽ��_________________��������Ķ����ϻ�ͼ����������ש����ͼ��ͼ��������輸��ֱ�۵Ľ���.
�ĵ�ʽд�����������ĺ͵�ƽ��_________________��������Ķ����ϻ�ͼ����������ש����ͼ��ͼ��������輸��ֱ�۵Ľ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com