
【题目】已知:直线AB∥CD,点E. F分别是AB、CD上的点。
(1)如图1,当点P在AB、CD内部时,试说明:∠EPF=∠AEP+∠CFP;
(2)如图2,当点P在AB上方时,∠EPF、∠AEP、∠CFP之间有怎样的数量关系?并说明理由。


科目:初中数学 来源: 题型:
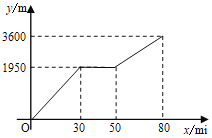
【题目】小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
⑴小亮行走的总路程是____________cm,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
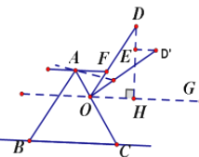
【题目】图 1 是小红在“淘宝双 11”活动中所购买的一张多档位可调节靠椅,档位调节示意图如图 2 所示。已知两支脚 AB=AC,O 为 AC 上固定连接点,靠背 OD=10 分米。档位为Ⅰ档时,OD∥AB,档位为Ⅱ挡时,OD’⊥AC,过点O作OG∥BC,则∠DOG+∠D’OG=_________°当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端 D 向后靠至 D’,此时点 D 移动的水平距离是 2 分米,即 ED’=2 分米。DH⊥OG于点H,则D到直线OG的距离为_________ 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改进银行的服务质量,随机抽随机抽查了![]() 名顾客,统计了顾客在窗口办理业务所用的时间(单位:分钟)下图是这次调查得到的统计图。
名顾客,统计了顾客在窗口办理业务所用的时间(单位:分钟)下图是这次调查得到的统计图。

请你根据图中的信息回答下列问题:
(1)求办理业务所用的时间为![]() 分钟的人教;
分钟的人教;
(2)补全条形统计图;
(2)求这![]() 名顾客办理业务所用时间的平均数.
名顾客办理业务所用时间的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为长方形,C点在x轴,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),长方形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,F(2,4).
(1)求G点坐标;
(2)△EFG的面积为 (直接填空);
(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的纵坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜![]() 个、乙种书柜
个、乙种书柜![]() 个,共需资金
个,共需资金![]() 元;若购买甲种书柜
元;若购买甲种书柜![]() 个,乙种书柜
个,乙种书柜![]() 个,共需资金
个,共需资金![]() 元
元
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共![]() 个,学校至多能够提供资金
个,学校至多能够提供资金![]() 元,请设计几种购买方案供这个学校选择.(两种规格的书柜都必须购买)
元,请设计几种购买方案供这个学校选择.(两种规格的书柜都必须购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中
中![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() 绕点
绕点![]() 自由旋转.
自由旋转.

(1)当![]() 在
在![]() 边上时,
边上时,
①线段![]() 和线段
和线段![]() 的关系是____________________;
的关系是____________________;
②若![]() ,则
,则![]() 的度数为____________;
的度数为____________;
(2)如图2,点![]() 不在
不在![]() 边上,
边上,![]() ,
,![]() 相交于点
相交于点![]() ,(l)问中的线段
,(l)问中的线段![]() 和线段
和线段![]() 的关系是否仍然成立?并说明理由.
的关系是否仍然成立?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com