
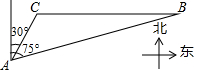
 如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321) 分析 先延长BC交AE于D,则∠ADC=90°,根据∠CAD=30°,AC=100,可得CD=$\frac{1}{2}$AC=50,AD=cos30°×AC=50$\sqrt{3}$,再根据Rt△ABD中,tan∠BAD=$\frac{BD}{AD}$,即可得到BC的长.
解答  解:如图所示,延长BC交AE于D,则∠ADC=90°,
解:如图所示,延长BC交AE于D,则∠ADC=90°,
∵∠CAD=30°,AC=100,
∴CD=$\frac{1}{2}$AC=50,AD=cos30°×AC=50$\sqrt{3}$,
∵Rt△ABD中,tan∠BAD=$\frac{BD}{AD}$,
∴3.7321≈$\frac{50+BC}{50\sqrt{3}}$,
解得BC≈273.2,
答:观光小岛BC之间的距离为273.2米.
点评 本题主要考查了解直角三角形的应用,在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
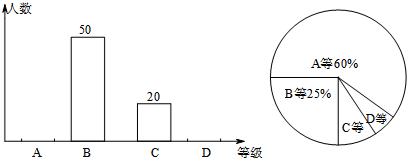
| A. | 样本容量是200 | |
| B. | 样本中C等所占百分比是10% | |
| C. | D等所在扇形的圆心角为15° | |
| D. | 估计全校学生成绩为A等大约有900人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
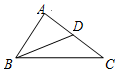 如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com