
���� ��1������һ�ԡ������㡱������Ϊ��a��b���ͣ�b��a�����ٵ�ab=0ʱ�����Dz������ڷ�����������ͼ���ϣ��ڵ�ab��0ʱ����$b=\frac{k}{a}$�ɵ�$a=\frac{k}{b}$�����ǵõ����ۣ�
��2����M��m��n����N��n��m������y=cx+d�����ɵõ����ۣ�
��3�����A��p��q������$q=-\frac{2}{p}$����ֱ��AB������P��$\frac{1}{2}$��$\frac{1}{2}$�����õ�p+q=1���õ�q=-1��q=2������һ�ԡ������㡱����y=x2+bx+c�ã����ǵõ����ۣ�
��� �⣺��1����һ����
����һ�ԡ������㡱������Ϊ��a��b���ͣ�b��a����
�ٵ�ab=0ʱ�����Dz������ڷ�����������ͼ���ϣ�
�ڵ�ab��0ʱ����$b=\frac{k}{a}$�ɵ�$a=\frac{k}{b}$������a��b���ͣ�b��a�����ڷ���������$y=\frac{k}{x}$��k��0����ͼ���ϣ�
��2����M��m��n����N��n��m������ֱ��MN�ı���ʽΪy=cx+d��c��0����
����$\left\{\begin{array}{l}mc+d=n\\ nc+d=m\end{array}\right.$���$\left\{\begin{array}{l}c=-1\\ d=m+n\end{array}\right.$��
��ֱ��MN�ı���ʽΪy=-x+m+n��
��3�����A��p��q������$q=-\frac{2}{p}$��
��ֱ��AB������P��$\frac{1}{2}$��$\frac{1}{2}$�����ɣ�2����$\frac{1}{2}=-\frac{1}{2}+p+q$��
��p+q=1��
��$p-\frac{2}{p}=1$��
�Ⲣ����ã�p=2��p=-1��
��q=-1��q=2��
����һ�ԡ������㡱�ǣ�2��-1���ͣ�-1��2����
����һ�ԡ������㡱����y=x2+bx+c�ã�
��$\left\{\begin{array}{l}1-b+c=2\\ 4+2b+c=-1\end{array}\right.$���$\left\{\begin{array}{l}b=-2\\ c=-1\end{array}\right.$��
��������ߵı���ʽΪy=x2-2x-1��
���� ���⿼���˷���������ͼ���ϵ����������������ϵ���������Ľ���ʽ����ȷ�����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
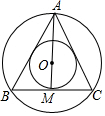 ��ͼ�ȱ�������ABC�У�AB=6��AMΪ��BC�ϵ����ߣ�OΪ���ģ����ABC���Բ�İ뾶������Բ�İ뾶��
��ͼ�ȱ�������ABC�У�AB=6��AMΪ��BC�ϵ����ߣ�OΪ���ģ����ABC���Բ�İ뾶������Բ�İ뾶���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| 45-47 | 47-49 | 49-51 | 51-53 | 53-55 | |
| Aũ������ | 2 | 8 | 15 | 10 | 5 |
| Bũ������ | 4 | 6 | 12 | 14 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
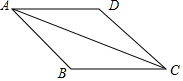 ��֪����ͼ����BAD=��DCB����BAC=��DCA��
��֪����ͼ����BAD=��DCB����BAC=��DCA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com