
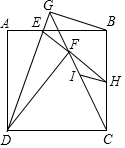
 如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$.
如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$. 分析 建立如图坐标系,作FM⊥AB于M,延长MF交CD于N,连接DH.只要证明HI是△CBG的中位线,求出BG的长即可解决问题.
解答 解:建立如图坐标系,作FM⊥AB于M,延长MF交CD于N,连接DH.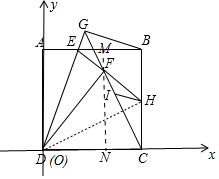
易证△DEA≌△DEF,△DHF≌△DHC,
∴AE=EF=1,FH=HC,设FH=HC=x,
在Rt△BEH中,∵EH2=EB2+BH2,
∴(x+1)2=22+(3-x)2,
∴x=$\frac{3}{2}$,
∴BH=CH,
由△FDN∽△EHB,
∴$\frac{DF}{EH}$=$\frac{FN}{EB}$=$\frac{DN}{BH}$,
∴$\frac{3}{\frac{5}{2}}$=$\frac{FN}{2}$=$\frac{DN}{\frac{3}{2}}$,
∴DN=$\frac{9}{5}$,FN=$\frac{12}{5}$,
∴F($\frac{9}{5}$,$\frac{12}{5}$),
∴直线CF的解析式为y=-2x+6,直线DE的解析式为y=3x,
由$\left\{\begin{array}{l}{y=3x}\\{y=-2x+6}\end{array}\right.$可得G($\frac{6}{5}$,$\frac{18}{5}$),
∴BG=$\frac{3}{5}$$\sqrt{10}$,
∵IH∥BG,CH=BH,
∴CI=GI,
∴GI=$\frac{1}{2}$BG=$\frac{3}{10}$$\sqrt{10}$,
故答案为$\frac{3}{10}$$\sqrt{10}$.
点评 本题考查翻折变换、正方形的性质、勾股定理、三角形的中位线定理、一次函数的应用,解题的关键是学会构建平面直角坐标系,利用方程组求两个函数的交点坐标,属于中考填空题中的压轴题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:
下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
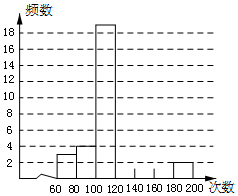 校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:| 次数分组 | 频数 |
| 60≤x<80 | 3 |
| 80≤x<100 | 4 |
| 100≤x<120 | 19 |
| 120≤x<140 | 10 |
| 140≤x<160 | 8 |
| 160≤x<180 | 4 |
| 180≤x<200 | 2 |
| 合计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 200 | 300 | 400 | 500 | 800 | 1000 |
| 摸到白球的次数m | 117 | 186 | 242 | 296 | 483 | 599 |
| 摸到白球的频率 $\frac{n}{m}$ | 0.585 | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com