
【题目】已知等腰Rt△ABC中,∠ACB=90°,AC=BC,点G在BC上,连接AG,过C作CF⊥AG,垂足为点E,过点B作BF⊥CF于点F,点D是AB的中点,连接DE、DF.
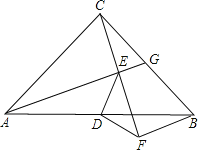
(1)若∠CAG=30°,EG=1,求BG的长;
(2)求证:∠AED=∠DFE.
【答案】(1)2![]() ﹣2(2)证明见解析
﹣2(2)证明见解析
【解析】
试题分析:(1)首先根据勾股定理求出CE的长,进而得到AC的长,因为AC=BC,所以BC可求,利用BH=BC﹣CG计算即可;
(2)连接CD,通过证明分别证明△ACE≌△CBF和△DCE≌△DBF,利用全等三角形的性质即可证明∠AED=∠DFE.
(1)解:∵∠CAG=∠FCB=30°,EG=1,sin30°=![]() =
=![]()
∴CG=2,
∴CE=![]() =
=![]()
∵sin30°=![]() ,
,
∴AC=2![]() ,
,
∴BC=2![]()
∴BG=2![]() ﹣2;
﹣2;
(2)证明:连接CD,
在△ACE和△CBF中,
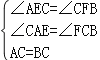 ,
,
∴△ACE≌△CBF(AAS),
∴CE=BF,
∵等腰RT△ABC中,点D是AB的中点,
∴CD=BD,
∵CD⊥BD,
∠DCE+∠DPC=∠FBP+∠FPB=90°,
∴∠DCE=∠DBF,
在△DCE和△DBF中,

∴△DCE≌△DBF(SAS),
∴∠CED=∠BFD,
∵∠AEC=∠CFB=90°,
∴∠AED=∠DFE.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
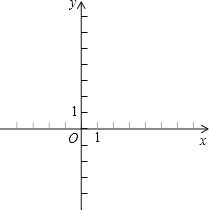
【题目】已知直线y1=2x+2及直线y2=﹣x+5,.
(1)直线y2=﹣x+5与y轴的交点坐标为 .
(2)在所给的平面直角坐标系(如图)中画出这两条直线的图象;
(3)求这两条直线以及x轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四种说法:①线段AB是点A与点B之间的距离;②射线AB与射线BA表示同一条射线;③两点确定一条直线;④两点之间线段最短.其中正确的个数是 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△AB C沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
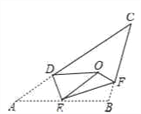
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com