
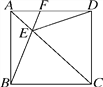
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
【答案】(1)见解析;(2)105°
【解析】试题分析:(1)根据正方形的性质可得BC=CD,∠ECB=∠ECD=45°,利用全等三角形的判定方法判定△BEC≌△DEC,(2)根据全等三角形的性质可得∠BEC=∠DEC= ![]() ,因为∠BED=120°,所以∠BEC=60°=∠AEF,
,因为∠BED=120°,所以∠BEC=60°=∠AEF,
所以∠EFD=60°+45°=105°.
试题解析: (1)证明:∵四边形ABCD是正方形,∴BC=CD,∠ECB=∠ECD=45°,
∴在△BEC与△DEC中,
 ,
,
∴△BEC≌△DEC(SAS),
(2)∵△BEC≌△DEC,
∴∠BEC=∠DEC= ![]() ,
,
∵∠BED=120°,
∴∠BEC=60°=∠AEF,
∴∠EFD=60°+45°=105°.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
(1)已知:点P(3,﹣4),求点P的坐标距离d(P)的值.
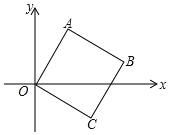
(2)如图,四边形OABC为正方形,且点A、B在第一象限,点C在第四象限.
①求证:d(A)=d(C).
②若OC=2,且满足d(A)+d(C)=d(B)+2,求点B坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( ) 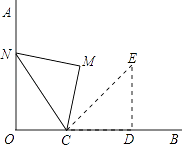
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出 平面内不在同一条直线上的三点确定一个面,那么平面内的四点(任意三点均不在同一直线上),能否在同一个面上呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时. 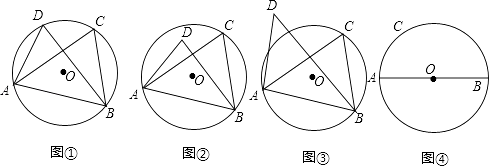
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 .
如图②,若点D在⊙O内,此时有∠ACB∠ADB;
如图③,若点D在⊙O外,此时有∠ACB∠ADB(填“=”、“>”、“<”)
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形. 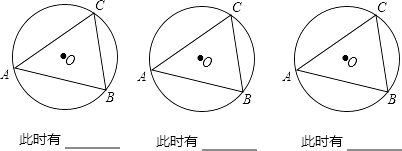
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线? 已知:如图,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB
作法:①连接CA、CB
②在CB上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB与M;
⑤连接D、M并延长,交⊙O于N,连接CN,则CN⊥AB.
请安上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)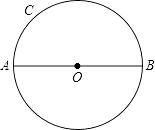
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( ) 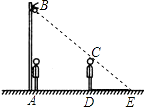
A.4米
B.5.6米
C.2.2米
D.12.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是![]() cm,则BC的长是( )
cm,则BC的长是( )
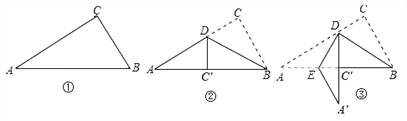
A. 3cm B. 4cm C. 5cm D. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=8 ![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= . 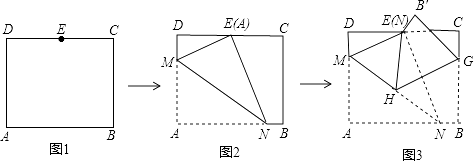
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.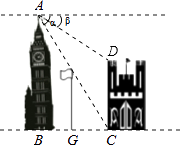
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市初中学生上学的交通方式,从中随机调查了a名学生的上学交通方式,统计结果如图. 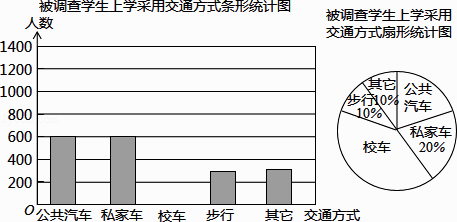
(1)求a的值;
(2)补全条形统计图并求出乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数;
(3)该市共有初中学生15000名,请估计其中坐校车上学的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com