
����Ŀ��С������ѧϰ�����ľ��飬�Ժ���y=x+![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=x+![]() ���Ա���x��ȡֵ��Χ��_____��
���Ա���x��ȡֵ��Χ��_____��
��2���±��г���y��x�ļ����Ӧֵ����д��m��n��ֵ��m=_____��n=_____��
x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| 1 | 2 | 3 | 4 | �� |
y | �� | �� | �� | ��2 | �� | �� | m |
| 2 |
| n |
| �� |
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ����
��4����Ϻ�����ͼ������ɣ�
�ٵ�y=��![]() ʱ��x=_____��
ʱ��x=_____��
��д���ú�����һ������_____��
��������x+![]() =t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
=t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
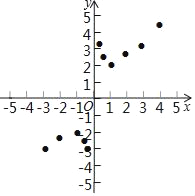
���𰸡���1��x��0����2��![]() ��
��![]() ����3������������4������4��
����3������������4������4��![]() ���ں���ͼ���ڵ�һ���������ҹ���ԭ��Գ�����t����2��t��2��
���ں���ͼ���ڵ�һ���������ҹ���ԭ��Գ�����t����2��t��2��
��������
��1���ɷ�ĸ��Ϊ0���ɵ��Ա���x��ȡֵ��Χ��x��0.
��2������ͼ����֪��m��n�ֱ�Ϊ��![]() ��x=3ʱ�ĺ���ֵ���������ʽ��
��x=3ʱ�ĺ���ֵ���������ʽ��![]() ����.
����.
��3����������ĵ�����ƽ����������.
��4���ٹ۲캯��ͼ���(2)�еı����У���![]() ʱ��x=4��
ʱ��x=4��![]() �ɵã���
�ɵã���![]() ʱ��x=-4��
ʱ��x=-4��![]() .
.
�ڹ۲캯����ͼ��д��������һ�����ʼ��ɣ������ԡ��Գ��ԡ�ͼ���������ȣ�.
�۴˷��̵ĸ��ɿ���![]() ��y=t�Ľ��㣬�ʷ�������������ȵ�ʵ�����ɿ���������������ͼ�����������㣬�۲�ͼ���֪����t>2��t<-2ʱ��������ͼ�����������㣬��t��ȡֵ��ΧΪ��t>2��t<-2.
��y=t�Ľ��㣬�ʷ�������������ȵ�ʵ�����ɿ���������������ͼ�����������㣬�۲�ͼ���֪����t>2��t<-2ʱ��������ͼ�����������㣬��t��ȡֵ��ΧΪ��t>2��t<-2.
�⣺��1����x�ڷ�ĸ�ϣ�
��x��0��
�ʴ�Ϊ��x��0��
��2����x=![]() ʱ��y=x+
ʱ��y=x+![]() =
=![]() ��
��
��x=3ʱ��y=x+![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3��������ߣ���������ͼ����
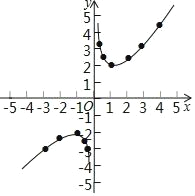
��4���ٵ�y=��![]() ʱ����x+
ʱ����x+![]() =��
=��![]() ��
��
��ã�x1=��4��x2=��![]() ��
��
�ʴ�Ϊ����4��![]() ��
��
�ڹ۲캯��ͼ��֪������ͼ���ڵ�һ���������ҹ���ԭ��Գƣ�
�ʴ�Ϊ������ͼ���ڵ�һ���������ҹ���ԭ��Գƣ�
�ۡ�x+![]() =t����������ȵ�ʵ������
=t����������ȵ�ʵ������
��t����2��t��2��
�ʴ�Ϊ��t����2��t��2��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
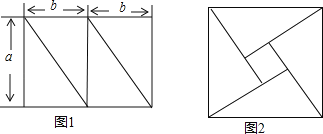
����Ŀ����֪���߳��ֱ�Ϊa��2b��a��b���ij����ηָ���ĸ�ȫ�ȵ�ֱ�������Σ���ͼ1���������ĸ�������ƴ����ͼ2��ʾ�������Σ��м��γ�һ�������εĿն����������ó����ε����Ϊ24�������εı߳�Ϊ5����ͨ�����ȡ����Ϣ����a2+b2��a2��b2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ACDE��֤�����ɶ���ʱ�õ���һ��ͼ�Σ�a��b��c��Rt��ABC��Rt��BED�߳�����֪AE=![]() c����ʱ���ǰѹ���x������ax+
c����ʱ���ǰѹ���x������ax+![]() cx+b=0��һԪ���η��̳�Ϊ����ϵһԪ���η��̡�.
cx+b=0��һԪ���η��̳�Ϊ����ϵһԪ���η��̡�.

��������������
д��һ������ϵһԪ���η��̡���
��֤������x�ġ���ϵһԪ���η��̡�ax+![]() cx+b=0����ʵ������
cx+b=0����ʵ������
��x=1�ǡ���ϵһԪ���η��̡�ax+![]() cx+b=0��һ���������ı���ACDE���ܳ���
cx+b=0��һ���������ı���ACDE���ܳ���![]() ������ABC���.
������ABC���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
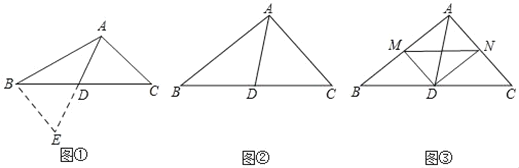
����Ŀ���������龳����ͼ�٣��ڡ�ABC�У���AB=10��AC=6����BC���ϵ�����AD��ȡֵ��Χ��
��1�������������ӳ�AD����EʹDE=AD��������BE����ACD���ŵ�D��ʱ����ת180���õ���EBD������AB��AC��2AD�����ڡ�ABE�У��������������ߵĹ�ϵ�����жϳ�����AD��ȡֵ��Χ���� ����
����˼������ʱ�����������������е����������������������Կ��ǹ����Ը��е�Ϊ�Գ����ĵ����ĶԳ�ͼ�Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬ���������У��Ӷ�������⣮
��2��������Ӧ�ã���ͼ�ڣ���ABC�У���BAC=90����AD��BC���ϵ����ߣ��Բ����߶�AB��AC��AD֮���������ϵ����˵�����ɣ�
��3������չ���죩��ͼ�ۣ���ABC�У���BAC=90����D��BC���е㣬DM��DN��DM��AB�ڵ�M��DN��AC�ڵ�N������MN����BM=4��MN=5��AC=6ʱ����ֱ��д������AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
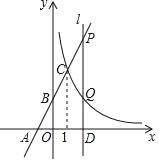
����Ŀ����ͼ��ֱ��y=kx+2��x�ᣬy��ֱ��ڵ�A����1��0���͵�B���뷴��������y=![]() ��ͼ���ڵ�һ�����ڽ��ڵ�C��1��n����
��ͼ���ڵ�һ�����ڽ��ڵ�C��1��n����
��1����һ�κ���y=kx+2�뷴��������y=![]() �ı���ʽ��
�ı���ʽ��
��2����x���ϵĵ�D��a��0����ƽ����y���ֱ��l��a��1�����ֱ���ֱ��y=kx+2��˫����y=![]() ����P��Q���㣬��PQ=2QD�����D�����꣮
����P��Q���㣬��PQ=2QD�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪����y=![]() ��k��0��x��0����ͼ����һ�κ���y=mx+5��m��0����ͼ���ཻ��ͬ�ĵ�A��B������A��AD��x���ڵ�D������AO�����е�A�ĺ�����Ϊx0����AOD�����Ϊ2��
��k��0��x��0����ͼ����һ�κ���y=mx+5��m��0����ͼ���ཻ��ͬ�ĵ�A��B������A��AD��x���ڵ�D������AO�����е�A�ĺ�����Ϊx0����AOD�����Ϊ2��
��1����k��ֵ��x0=4ʱm��ֵ��
��2����[x]��ʾΪ������x��������������磺[1.4]=1��[2]=2����t=ODDC������![]() ��m����
��m����![]() ����[m2t]ֵ��
����[m2t]ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�У�AB��4����E��F�ڶԽ���BD�ϣ�AE��CF��
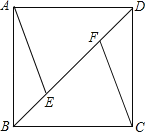
��1����֤����ABE�ա�CDF��
��2������ABE��2��BAE����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��ʾ����֪![]() �У�
�У�![]() ��ƽ�����ཻ�ڵ�
��ƽ�����ཻ�ڵ�![]() ,�Բ���
,�Բ���![]() ��
��![]() �Ĺ�ϵ����֤��.
�Ĺ�ϵ����֤��.
(2)��ͼ��ʾ����![]() �У�
�У�![]() �ֱ���
�ֱ���![]() �����ƽ���ߣ��Բ���
�����ƽ���ߣ��Բ���![]() ��
��![]() �Ĺ�ϵ_____ (ֱ��д�����Ҫ֤��)
�Ĺ�ϵ_____ (ֱ��д�����Ҫ֤��)
(3)��ͼ��ʾ����֪![]() Ϊ
Ϊ![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() Ϊ
Ϊ![]() ���
���![]() ��ƽ���ߣ�����
��ƽ���ߣ�����![]() ���ڵ�
���ڵ�![]() ,�Բ���
,�Բ���![]() ��
��![]() �Ĺ�ϵ_____ (ֱ��д�����Ҫ֤��)
�Ĺ�ϵ_____ (ֱ��д�����Ҫ֤��)
��1��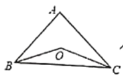 ��2��
��2�� 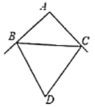 ��3��
��3�� 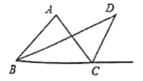
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���![]() ������ʵ����x1��x2����
������ʵ����x1��x2����![]() ʱ��m��ֵΪ_____________��
ʱ��m��ֵΪ_____________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com