
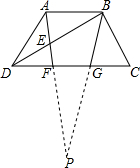
 在梯形ABCD中,AB∥CD,点F,G是下底CD的三等分点,BG与AF的延长线交于点P,AF与BD交于点E,求证:PF•AE=PA•EF.
在梯形ABCD中,AB∥CD,点F,G是下底CD的三等分点,BG与AF的延长线交于点P,AF与BD交于点E,求证:PF•AE=PA•EF. 分析 由AB∥CD,得到△ABE∽△DEF,△ABP∽△FGP,求得$\frac{AE}{EF}=\frac{AB}{DF}$,$\frac{AB}{FG}=\frac{PA}{PF}$,等量代换得到$\frac{AE}{EF}=\frac{PA}{PF}$,于是得到结论.
解答 解:∵AB∥CD,
∴△ABE∽△DEF,△ABP∽△FGP,
∴$\frac{AE}{EF}=\frac{AB}{DF}$,$\frac{AB}{FG}=\frac{PA}{PF}$,
∵点F,G是下底CD的三等分点,
∴DF=FG,
∴$\frac{AE}{EF}=\frac{PA}{PF}$,
∴PF•AE=PA•EF.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
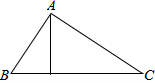 如图,点A表示一个半径为400米的森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=37°,如果在两村庄之间修一条长1000m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?请说明理由.(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
如图,点A表示一个半径为400米的森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=37°,如果在两村庄之间修一条长1000m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?请说明理由.(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
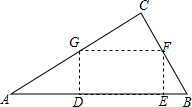 如图,在直角△ABC中,∠C=90°,AC=8,BC=6,在△ABC中裁剪出矩形DEFG.则下列结论一定成立的是①②(把所有正确结论的序号都填在横线上).
如图,在直角△ABC中,∠C=90°,AC=8,BC=6,在△ABC中裁剪出矩形DEFG.则下列结论一定成立的是①②(把所有正确结论的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com