Question

16．如图1，已知正方形ABCD在直线MN的上方，BC在直线MN上，E是射线BC上一点，以AE为边在直线MN的上方作正方形AEFG．
（1）连接FC，观察并猜测tan∠FCN的值，并说明理由；
（2）如图2，将图1中正方形ABCD改为矩形ABCD，AB=m，BC=n（m，n为常数），E是射线BC上一动点（不含端点B），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上，当点E沿射线CN运动时，请用含m，n的代数式表示tan∠FCN的值．   

Answer 1

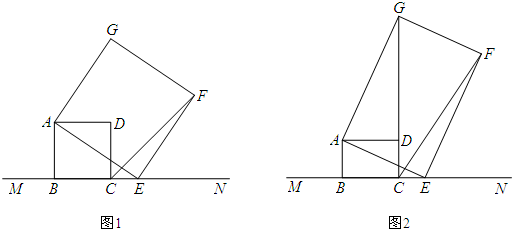
分析 （1）过F作FH⊥MN于H，由条件可证明△EHF≌△ABE，可证得CH=BE=FH，可求得∠FCH=45°，可求得tan∠FCN=1；
（2）过F作FH⊥MN于H，可证明△EFH≌△AGD，进一步可证明△EFH∽△AEB，结合相似三角形的性质可得$\frac{EH}{AB}$=$\frac{FH}{BE}$=$\frac{FH}{CH}$，在Rt△FEH中，由三角函数的定义可求得答案．

解答 解：
（1）tan∠FCN=1，
理由是：如图1，作FH⊥MN于H，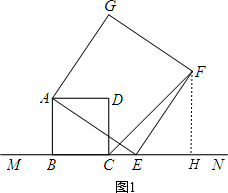

∵∠AEF=∠ABE=90°，
∴∠BAE+∠AEB=90°，∠FEH+∠AEB=90°，
∴∠FEH=∠BAE，
在△EHF和△ABE中
$\left\{\begin{array}{l}{∠EHF=∠ABE}\\{∠FEH=∠BAE}\\{EF=AE}\end{array}\right.$，
∴△EHF≌△ABE（AAS），
∴FH=BE，EH=AB=BC，
∴CH=BE=FH，
∵∠FHC=90°，
∴tan∠FCH=$\frac{FH}{CH}$=1；

（2）如图（2）作FH⊥MN于H．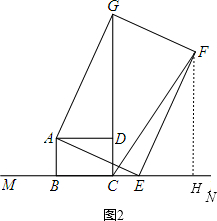

由已知可得∠EAG=∠BAD=∠AEF=90°，
结合（1）易得∠FEH=∠BAE=∠DAG，
又∵G在射线CD上，
∠GDA=∠EHF=∠EBA=90°，
在△EFH和△AGD中
$\left\{\begin{array}{l}{∠FHE=∠GDA}\\{∠FEH=∠DAG}\\{EF=AG}\end{array}\right.$，
∴△EFH≌△AGD（AAS），
∵∠BAE=∠FEH，∠ABE=∠FHE，
∴△EFH∽△AEB，
∴EH=AD=BC=n，∴CH=BE，
∴$\frac{EH}{AB}$=$\frac{FH}{BE}$=$\frac{FH}{CH}$，
∴在Rt△FEH中，tan∠FCN=$\frac{FH}{CH}$=$\frac{EH}{AB}$=$\frac{n}{m}$，
∴当点E沿射线CN运动时，tan∠FCN=$\frac{n}{m}$．

点评 本题主要考查矩形、正方形的性质及全等三角形、相似三角形的判定和性质、三角函数的定义的综合应用．本题是一个类比探究问题，需要调用处理类比探究的思路（照搬字母，照搬辅助线，照搬思路）来解决问题；要求角度的正切值，首先把角放到直角三角形中，作出需要的辅助线，表达出角度的正切值；观察图形结构，利用“一线三等角”出现全等或相似来转化比例关系，考虑线段关系复杂，采用量化的手段来减轻思维量；照搬第一问的思路去解决第二问，类比不下去时，需要考虑图形中有哪些不变特征（一线三等角不变），同时考虑新增加的条件是什么（点G在射线CD上），找思路解决．