
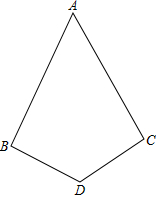
 如图已知:AB=AC.DB=DC,∠ABD=∠ACD.试判断直线AD、BC的位置关系并加以证明.
如图已知:AB=AC.DB=DC,∠ABD=∠ACD.试判断直线AD、BC的位置关系并加以证明. 科目:初中数学 来源: 题型:选择题
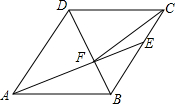 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
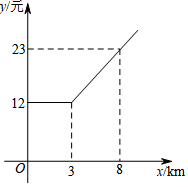 为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:
为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )| A. | (-4,-1) | B. | (-1,-4) | C. | (5,-4) | D. | (-5,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
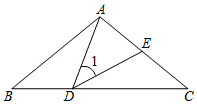 如图,△ABC中,AB=AC=5cm,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
如图,△ABC中,AB=AC=5cm,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
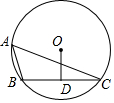 如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )
如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )| A. | 1 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com