
| A.最大值-5 | B.最小值-5 | C.最大值-6 | D.最小值-6 |
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
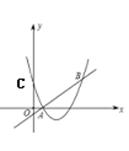
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
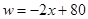 ,设销售这种台灯每天的利润为y(元).
,设销售这种台灯每天的利润为y(元).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 x+150,成本为40元/件,无论销售多少,每月还需支出房租费52500元,设月利润为w专(元)(利润 = 销售额-成本-广告费).若只是电视直销,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,40≤a≤80),当月销量为x(件)时,每月还需缴纳
x+150,成本为40元/件,无论销售多少,每月还需支出房租费52500元,设月利润为w专(元)(利润 = 销售额-成本-广告费).若只是电视直销,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,40≤a≤80),当月销量为x(件)时,每月还需缴纳 x2 元的广告费,设月利润为w电(元)(利润 = 销售额-成本-附加费).
x2 元的广告费,设月利润为w电(元)(利润 = 销售额-成本-附加费).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com