
【题目】“若抛物线y=ax2+bx+c与x轴有两个交点,则一元二次方程ax2+bx+c=0有两个不等实根。”请根据你对这句话的理解,解决下面问题:若d、e(d<e)是关于x的方程1+(x﹣f)(x﹣g)=0的两根,且f<g,则d、e、f、g的大小关系是________.
【答案】f<d<e<g
【解析】
依题意画出函数y=(x﹣f)(x﹣g)图象草图,根据二次函数的增减性求解.
解:依题意,画出函数y=(x﹣f)(x﹣g)的图象,如图所示.
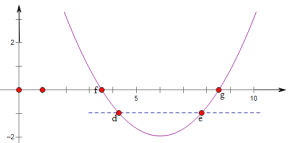
函数图象为抛物线,开口向上,与x轴两个交点的横坐标分别为f,g(f<g).
方程1+(x﹣f)(x﹣g)=0
转化为(x﹣f)(x﹣g)=-1,
方程的两根是抛物线y=(x﹣f)(x﹣g)与直线y=-1的两个交点.
由d<e,可知对称轴左侧交点横坐标为d,右侧为e.
由抛物线开口向上,则在对称轴左侧,y随x增大而减少,则有f<d;在对称轴右侧,y随x增大而增大,则有e<g.
综上所述,可知f<d<e<g.
故答案为:f<d<e<g.


科目:初中数学 来源: 题型:
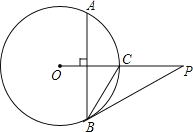
【题目】如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
若![]() ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)点(﹣5,﹣2)的“可控变点”坐标为 ;
(2)若点P在函数![]() 的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;
的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;
(3)若点P在函数![]() (
(![]() )的图象上,其“可控变点”Q的纵坐标y′ 的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′ 的取值范围是![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
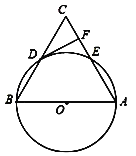
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.若小文早餐吃了两个粽子,求这两个粽子刚好都是花生馅粽的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
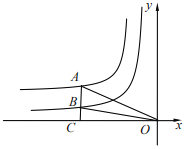
【题目】如图,点A是反比例图数y=![]() (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y=
(x<0)图象上一点,AC⊥x轴于点C,与反比例函数y=![]() (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
(x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
A.﹣4B.﹣6C.﹣8D.﹣12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com