
分析 (1)由题意得$\left\{\begin{array}{l}{-k+b=-(k-6)}\\{-2k+b=-\frac{k-6}{2}}\end{array}\right.$,解方程组即可求得k、b的值,从而求得解析式;
(2)从正数,负数中各选几个值作为x的值,进而得到y的值,描点,连线即可画出反比例函数的图象,然后根据两点画出直线即可;
(3)根据图象即可求得.
解答 解:(1)由题意得$\left\{\begin{array}{l}{-k+b=-(k-6)}\\{-2k+b=-\frac{k-6}{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=2}\\{b=6}\end{array}\right.$,
∴这两个函数的解析式为y1=2x+6,y2=-$\frac{4}{x}$;
(2)画出这两个函数的图象如图: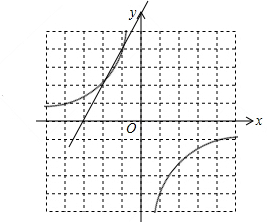
(3)由图象可知:
①-2≤x≤-1或x>0;
②0<y≤2.
故答案为:-2≤x≤-1;0<y≤2.
点评 本题考查了反比例函数和一次函数的交点问题以及画出函数的图象;根据题意列出方程组是解题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题
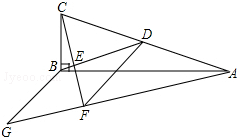 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
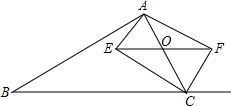 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com