
����Ŀ����֪������![]() �У�
��![]() ��
��![]() �Ĵ�ֱƽ��
�Ĵ�ֱƽ��![]() �߷ֱ�
�߷ֱ�![]() �ڵ�
�ڵ�![]() ������Ϊ
������Ϊ![]() ��
��
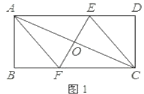
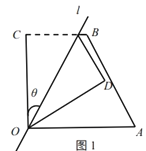
��1����ͼ1������![]() ����֤���ı���
����֤���ı���![]() Ϊ���Σ�
����
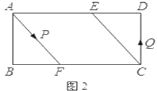
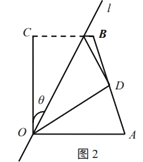
��2����ͼ2������![]() �ֱ��
�ֱ��![]() ����ͬʱ��������
����ͬʱ��������![]() ��
��![]() ���������˶�һ�ܣ�����
���������˶�һ�ܣ�����![]() ��
��![]() ֹͣ����
ֹͣ����![]() ��
��![]() ֹͣ�����˶������У�
ֹͣ�����˶������У�
����֪��![]() ���ٶ�Ϊÿ��
���ٶ�Ϊÿ��![]() ����
����![]() ���ٶ�Ϊÿ��
���ٶ�Ϊÿ��![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �룬��
�룬��![]() �ĵ�Ϊ������ı�����ƽ���ı���ʱ����
�ĵ�Ϊ������ı�����ƽ���ı���ʱ����![]() ____________��
____________��
������![]() ���˶�·�̷ֱ�Ϊ
���˶�·�̷ֱ�Ϊ![]() ����λ:
����λ:![]() ������֪
������֪![]() �ĵ�Ϊ������ı�����ƽ���ı��Σ���
�ĵ�Ϊ������ı�����ƽ���ı��Σ���![]() ��
��![]() �����������ϵʽΪ____________��
�����������ϵʽΪ____________��
���𰸡���1������������2����![]() ����
����![]()
��������
(1)��֤���ı���AFCEΪƽ���ı��Σ��ٸ��ݶԽ����ഹֱƽ�ֵ�ƽ���ı��������������ж���
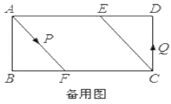
(2)�ٷ�������ۿ�֪����P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴�ɣ�
�ڷ�����������ۿ�֪a��b�����������ϵʽ.
��1��֤�������ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]()
��![]() ��
��
��![]() ��ֱƽ��
��ֱƽ��![]() ������Ϊ
������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
�֡�![]()
���ı���![]() Ϊ���Σ�
����
��2����![]() �룮
�룮
��Ȼ��![]() ����
����![]() ��ʱ��
��ʱ��![]() ����
����![]() �ϣ���ʱ
�ϣ���ʱ![]() �ĵ㲻���ܹ���ƽ���ı��Σ�ͬ��
�ĵ㲻���ܹ���ƽ���ı��Σ�ͬ��![]() ����
����![]() ��ʱ��
��ʱ��![]() ����
����![]() ��
���ϣ�Ҳ���ܹ���ƽ���ı��Σ����ֻ�е�
![]() ����
����![]() �ϡ�
�ϡ�![]() ����
����![]() ��ʱ�����ܹ���ƽ���ı��Σ�
��ʱ�����ܹ���ƽ���ı��Σ�
����![]() �ĵ�Ϊ������ı�����ƽ���ı���ʱ��
�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]()
���![]() ���ٶ�Ϊÿ��
���ٶ�Ϊÿ��![]() ����
����![]() ���ٶ�Ϊÿ��
���ٶ�Ϊÿ��![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �룬
�룬
��![]() ��
��
��![]() �����
�����![]()
����![]() �ĵ�Ϊ������ı�����ƽ���ı���ʱ��
�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��![]() ��
��![]() �����������ϵʽ��
�����������ϵʽ��![]() ��
��
������ã���![]() �ĵ�Ϊ������ı�����ƽ���ı���ʱ��
�ĵ�Ϊ������ı�����ƽ���ı���ʱ��
��![]() �ڻ���ƽ�еĶ�Ӧ���ϣ������������
�ڻ���ƽ�еĶ�Ӧ���ϣ������������
i����ͼ1����![]() ����
����![]() �ϡ�
�ϡ�![]() ����
����![]() ��ʱ��
��ʱ��![]() ����
����![]() ����
����![]() ��
��
ii����ͼ2����![]() ����
����![]() �ϡ�
�ϡ�![]() ����
����![]() ��ʱ��
��ʱ��![]() ����
����![]() ����
����![]() ��
��
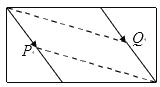
iii����ͼ3����![]() ����
����![]() �ϡ�
�ϡ�![]() ����
����![]() ��ʱ��
��ʱ��![]() ����
����![]() ����
����![]() ��
��
����������![]() ��
��![]() �����������ϵʽ��
�����������ϵʽ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
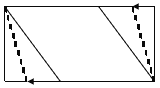
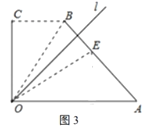
����Ŀ�����Ķ�����ͼ1���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ���ı��ηֳ������֣�ֱ��
���ı��ηֳ������֣�ֱ��![]() ��
��![]() ���ɵĽ���Ϊ
���ɵĽ���Ϊ![]() �����ı���
�����ı���![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() �۵�����
�۵�����![]() ���ڵ�
���ڵ�![]() �������ǰ�����������̼�Ϊ
�������ǰ�����������̼�Ϊ![]() ��
��
�����⣩����![]() ���
���![]() �غϣ��������������Ϊ
�غϣ��������������Ϊ![]() [__________��__________]��
[__________��__________]��
 ��������
��������  ��������
�������� 
�����ԣ�
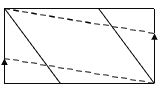
��1������![]() ǡΪ
ǡΪ![]() ���е�(��ͼ2)����
���е�(��ͼ2)����![]() ��
��
��2������![]() ��������
��������![]() ����
����![]() ��������
��������![]() ���ı���
���ı���![]() �ı�
�ı�![]() ��(��ͼ3)�����
��(��ͼ3)�����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
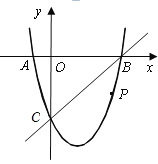
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�C��0����3������P��ֱ��BC�·��������ϵ�һ�����㣮
��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�C��0����3������P��ֱ��BC�·��������ϵ�һ�����㣮
��1������κ�������ʽ��
��2������PO��PC��������POC��y����ۣ��õ��ı���![]() .�Ƿ���ڵ�P��ʹ�ı���
.�Ƿ���ڵ�P��ʹ�ı���![]() Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
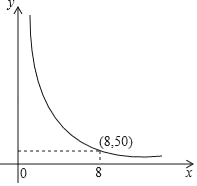
����Ŀ����ͷ����ÿ����һ���ִ���װ�ػ��ƽ��ÿ��װ���ٶ�y����/Ԫ����װ���������ʱ��x���죩֮���Ƿ�����������ϵ����ͼ����ͼ��ʾ��
��1������������������ı���ʽ��
��2�����ڽ��������Ҫ���ϵĻ��ﲻ����5��ж����ϣ���ôƽ��ÿ������Ҫж�����ٶ֣�
��3������ͷԭ�й���10������ÿ������ÿ���װж����ͬ��װ�����ǡ������8��ʱ�䣬�ڣ�2���������£�������Ҫ���Ӷ��������˲����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
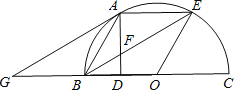
����Ŀ����ͼ����A��E�ǰ�Բ���ϵ����ȷֵ㣬ֱ��BC=2��AD��BC������ΪD������BE��AD��F����A��AG��BE��BC��G��
��1���ж�ֱ��AG����O��λ�ù�ϵ����˵�����ɣ�
��2�����߶�AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��y����һ��������x[]y=![]() ������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�������������㣬���磺0[]2=
������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�������������㣬���磺0[]2=![]() =��2b����֪1[]2=3����1[]3=��2�������������⣮
=��2b����֪1[]2=3����1[]3=��2�������������⣮
(1)��a��b��ֵ��
(2)��M=��m2��m��1��[]��2m��2m2�������M��m�ĺ��������Ա���m�ک�1��m��3�ķ�Χ��ȡֵʱ������ֵMΪ�����ĸ�����Ϊk����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij·����Ǧ�����ڵ�ʾ��ͼ������AC�ĸ�Ϊ11�ף��Ƹ�AB�����AC�ļнǡ�A=120����·�Ʋ����ε��֣��ڵ����ϵ���������DE��Ϊ18�ף���D��E�������·��B�����Ƿֱ�Ϊ����������tan��=6��tan��=![]() ����Ƹ�AB�ij��ȣ�
����Ƹ�AB�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�M��N��BD�����ȷֵ㣬����CM���ӳ���AB�ڵ�E������EN���ӳ���CD�ڵ�F�����½��ۣ�
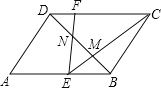
��EΪAB���е㣻
��FC=4DF��
��S��ECF=![]() ��
��
�ܵ�CE��BDʱ����DFN�ǵ��������Σ�
����һ����ȷ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
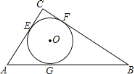
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��
(1)��![]() ����Բ�İ뾶��
����Բ�İ뾶��
(2)���ƶ�Բ��![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() ������
������![]() �ı�
�ı�![]() ��
��![]() ������
������
����뾶![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڵ�![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ʱ����Բ��
ʱ����Բ��![]() ��λ�ã�
��λ�ã�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com