
ЎѕМвДїЎїєРЦРУРИфёЙГ¶єЪЗтєН°ЧЗтЈ¬ХвР©ЗтіэСХЙ«НвОЮЖдЛыІо±рЈ¬ПЦИГС§ЙъЅшРРГюЗтКФСйЈєГїґОГюіцТ»ёцЗтЈ¬јЗПВСХЙ«єу·Е»ШТЎФИЈ¬ЦШёґЅшРРХвСщµДКФСйµГµЅТФПВКэѕЭЈє
ГюЖеµДґОКэn | 100 | 200 | 300 | 500 | 800 | 1000 |
ГюµЅєЪЖеµДґОКэm | 38 | 79 | 121 | 196 | 322 | 398 |
ГюµЅєЪЖеµДЖµВК | 0.380 | 0.395 | 0.403 | 0.392 | 0.403 | 0.398 |
ЈЁ1Ј©ёщѕЭ±нЦРКэѕЭ№АјЖЈ¬ґУєРЦРГюіцТ»ёцЗтКЗ°ЧЗтµДёЕВККЗ_____ЈЁѕ«И·µЅ0.01Ј©Ј»
ЈЁ2Ј©ИфєРЦРєЪЗтУл°ЧЗт№ІУР5Г¶Ј¬ДіН¬С§Б¬РшІ»·Е»ШµШГюіцБЅёцЗтЈ¬УГКчЧґНј»т±нёсјЖЛгХвБЅёцЗтСХЙ«І»Н¬µДёЕВКЈ®
Ўѕґр°ёЎї(1)0.60;(2)јыЅвОц.
ЎѕЅвОцЎї
ЈЁ1Ј©ґуБїЦШёґКФСйПВГюЗтµДЖµВКїЙТФ№АјЖГюЗтµДёЕВКЈ¬ѕЭґЛЗуЅвЈ»
ЈЁ2Ј©»КчЧґНјБРіцЛщУРµИїЙДЬЅб№ыЈ¬ФЩХТµЅ·ыєПМхјюµДЅб№ыКэЈ¬ёщѕЭёЕВК№«КЅЗуЅвїЙµГЈ®
ЅвЈєЈЁ1Ј©ёщѕЭ±нЦРКэѕЭ№АјЖґУєРЦРГюіцТ»ёцЗтКЗ°ЧЗтµДёЕВККЗ1©Ѓ0.40ЈЅ0.60Ј¬
№Кґр°ёОЄЈє0.60Ј»
ЈЁ2Ј©УЙЈЁ1Ј©їЙЦЄЈ¬єЪЗтµДёцКэОЄ5ЎБ0.40ЈЅ2Ј¬Фт°ЧЗтµДёцКэОЄ3Ј¬
»КчЧґНјИзПВЈє
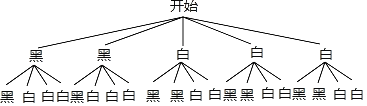
УЙ±нїЙЦЄЈ¬ЛщУРµИїЙДЬЅб№ы№ІУР20ЦЦЗйїцЈ¬
ЖдЦРХвБЅЗтСХЙ«І»Н¬µДУР12ЦЦЅб№ыЈ¬
ЛщТФХвБЅЗтСХЙ«І»Н¬µДёЕВКОЄ![]() Ј®
Ј®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄPЈЁЈ3Ј¬mЈ©єНQ(1Ј¬m)КЗЕЧОпПЯyЈЅ2x2Ј«bxЈ«1ЙПµДБЅµгЈ®
(1)ЗуbµДЦµЈ»
(2)ЕР¶П№ШУЪxµДТ»ФЄ¶юґО·ЅіМ2x2Ј«bxЈ«1ЈЅ0КЗ·сУРКµКэёщЈ¬ИфУРЈ¬ЗуіцЛьµДКµКэёщЈ»ИфГ»УРЈ¬ЗлЛµГчАнУЙЈ»
(3)Ѕ«ЕЧОпПЯyЈЅ2x2Ј«bxЈ«1µДНјПуПтЙПЖЅТЖk(kКЗХэХыКэЈ©ёцµҐО»Ј¬К№ЖЅТЖєуµДНјПуУлxЦбОЮЅ»µгЈ¬ЗуkµДЧоРЎЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЎчABCЦРЈ¬ЎПC=90ЎгЈ¬AB=9Ј¬![]() Ј¬°СЎчABC ИЖЧЕµгCРэЧЄЈ¬К№µГµгAВдФЪµгAЎдЈ¬µгBВдФЪµгBЎдЈ®ИфµгAЎдФЪ±ЯABЙПЈ¬ФтµгBЎўBЎдµДѕаАлОЄ_____Ј®
Ј¬°СЎчABC ИЖЧЕµгCРэЧЄЈ¬К№µГµгAВдФЪµгAЎдЈ¬µгBВдФЪµгBЎдЈ®ИфµгAЎдФЪ±ЯABЙПЈ¬ФтµгBЎўBЎдµДѕаАлОЄ_____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ѕШРОABCDЦРЈ¬ABЈЅ3Ј¬BCЈЅ4Ј¬Ѕ«ёГѕШРОСШ¶ФЅЗПЯBDХЫµюЈ¬ФтНјЦРТхУ°Ії·ЦµДГж»эКЗ¶аЙЩЈї
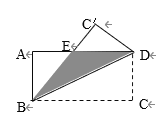
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯy=ax2 +bx+ 4УлxЦбµДБЅёцЅ»µг·Ц±рОЄAЈЁЈ4Ј¬0Ј©ЎўBЈЁ2Ј¬0Ј©Ј¬УлyЦбЅ»УЪµгCЈ¬¶ҐµгОЄDЈ®EЈЁ1Ј¬2Ј©ОЄПЯ¶ОBCµДЦРµгЈ¬BCµДґ№Ц±ЖЅ·ЦПЯУлxЦбЎўyЦб·Ц±рЅ»УЪFЎўGЈ®
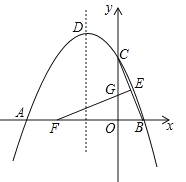
ЈЁ1Ј©ЗуЕЧОпПЯµДєЇКэЅвОцКЅЈ¬ІўРґіц¶ҐµгDµДЧш±кЈ»
ЈЁ2Ј©ФЪЦ±ПЯEFЙПЗуТ»µгHЈ¬К№ЎчCDHµДЦЬі¤ЧоРЎЈ¬ІўЗуіцЧоРЎЦЬі¤Ј»
ЈЁ3Ј©ИфµгKФЪxЦбЙП·ЅµДЕЧОпПЯЙПФЛ¶ЇЈ¬µ±KФЛ¶ЇµЅКІГґО»ЦГК±Ј¬
ЎчEFKµДГж»эЧоґуЈїІўЗуіцЧоґуГж»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ѕШРОABCDЦРЈ¬ABЈЅ6Ј¬BCЈЅ8Ј¬µгEКЗBC±ЯЙПТ»µгЈ¬Б¬ЅУAEЈ¬°СЎПBСШAEХЫµюЈ¬К№µгBВдФЪµгBЎдґ¦Ј¬µ±ЎчCEBЎдОЄЦ±ЅЗИэЅЗРОК±Ј¬BEµДі¤ОЄ_____Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄТ»ґОєЇКэyЈЅ©Ѓ![]() x+2µДНјПуЈ¬ИЖxЦбЙПТ»µгPЈЁmЈ¬0Ј©РэЧЄ180ЎгЈ¬ЛщµГµДНјПуѕ№эЈЁ0Ј®©Ѓ1Ј©Ј¬ФтmµДЦµОЄЈЁЎЎЎЎЈ©
x+2µДНјПуЈ¬ИЖxЦбЙПТ»µгPЈЁmЈ¬0Ј©РэЧЄ180ЎгЈ¬ЛщµГµДНјПуѕ№эЈЁ0Ј®©Ѓ1Ј©Ј¬ФтmµДЦµОЄЈЁЎЎЎЎЈ©
A.©Ѓ2B.©Ѓ1C.1D.2
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ№ШУЪxµДТ»ФЄ¶юґО·ЅіМ![]() Ј¬
Ј¬
ЈЁ1Ј©ЗуЦ¤ЈєёГТ»ФЄ¶юґО·ЅіМЧЬУРБЅёцКµКэёщЈ»
ЈЁ2Ј©ИфёГ·ЅіМЦ»УРТ»ёцРЎУЪ4µДёщЈ¬ЗуmµДИЎЦµ·¶О§Ј»
ЈЁ3Ј©Ифx1Ј¬x2ОЄ·ЅіМµДБЅёцёщЈ¬ЗТnЈЅx12+x22©Ѓ4Ј¬ЕР¶П¶Їµг![]() ЛщРОіЙµДКэНјПуКЗ·сѕ№эµг
ЛщРОіЙµДКэНјПуКЗ·сѕ№эµг![]() Ј¬ІўЛµГчАнУЙЈ®
Ј¬ІўЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїРЎГчёщѕЭС§П°єЇКэµДѕСйЈ¬¶ФєЇКэy=x+![]() µДНјПуУлРФЦКЅшРРБЛМЅѕїЈ®
µДНјПуУлРФЦКЅшРРБЛМЅѕїЈ®
ПВГжКЗРЎГчµДМЅѕї№эіМЈ¬ЗлІ№ідНкХыЈє
ЈЁ1Ј©єЇКэy=x+![]() µДЧФ±дБїxµДИЎЦµ·¶О§КЗ_____Ј®
µДЧФ±дБїxµДИЎЦµ·¶О§КЗ_____Ј®
ЈЁ2Ј©ПВ±нБРіцБЛyУлxµДјёЧй¶ФУ¦ЦµЈ¬ЗлРґіцmЈ¬nµДЦµЈєm=_____Ј¬n=_____Ј»
x | Ў | ©Ѓ3 | ©Ѓ2 | ©Ѓ1 | ©Ѓ | ©Ѓ |
|
| 1 | 2 | 3 | 4 | Ў |
y | Ў | ©Ѓ | ©Ѓ | ©Ѓ2 | ©Ѓ | ©Ѓ | m |
| 2 |
| n |
| Ў |
ЈЁ3Ј©ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ГиіцБЛТФЙП±нЦРёч¶Ф¶ФУ¦ЦµОЄЧш±кµДµгЈ¬ёщѕЭГиіцµДµгЈ¬»іцёГєЇКэµДНјПуЈ»
ЈЁ4Ј©ЅбєПєЇКэµДНјПуЈ¬ЗлНкіЙЈє
ўЩµ±y=©Ѓ![]() К±Ј¬x=_____Ј®
К±Ј¬x=_____Ј®
ўЪРґіцёГєЇКэµДТ»МхРФЦК_____Ј®
ўЫИф·ЅіМx+![]() =tУРБЅёцІ»ПаµИµДКµКэёщЈ¬ФтtµДИЎЦµ·¶О§КЗ_____Ј®
=tУРБЅёцІ»ПаµИµДКµКэёщЈ¬ФтtµДИЎЦµ·¶О§КЗ_____Ј®
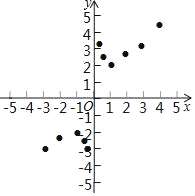
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com