
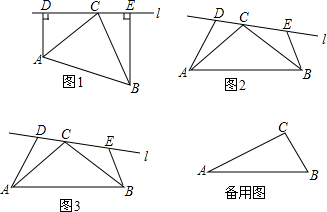
分析 (1)易证△ACD≌△CBE,则有AD=CE,CD=BE,从而可得DE=AD+BE;
(2)①易证△ADC∽△CEB,则有$\frac{AD}{CE}$=$\frac{CD}{BE}$=$\frac{AC}{BC}$=n,从而可得CE=$\frac{1}{n}$AD,CD=nBE,即可得到DE=DC+CE=$\frac{1}{n}$AD+nBE;
②同①可得CE=$\frac{1}{n}$AD,CD=nBE.由于直线l在绕着点C旋转过程中,点A到直线l的距离AD与点B到直线l的距离BE大小关系会发生变化,因此需分情况讨论(如图4、图5),然后只需结合图形就可解决问题.
解答 解:(1)【类比探究】猜想DE=AD+BE.
理由:如图2,
∵∠ADC=100°,
∴∠DAC+∠DCA=80°.
∵∠ACB=100°,
∴∠DCA+∠ECB=80°,
∴∠DAC=∠ECB.
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠ECB}\\{AC=CB}\end{array}\right.$,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∴DE=AD+BE;
(2)【拓展延伸】①猜想:DE=$\frac{1}{n}$AD+nBE.
理由:如图3,
∵∠ADC=100°,
∴∠DAC+∠DCA=80°.
∵∠ACB=100°,
∴∠DCA+∠ECB=80°,
∴∠DAC=∠ECB.
∵∠ADC=∠CEB,
∴△ADC∽△CEB,
∴$\frac{AD}{CE}$=$\frac{CD}{BE}$=$\frac{AC}{BC}$=n,
∴CE=$\frac{1}{n}$AD,CD=nBE,
∴DE=DC+CE=$\frac{1}{n}$AD+nBE;
②DE=$\frac{1}{n}$AD-nBE或DE=nBE-$\frac{1}{n}$AD.
提示:同①可得:CE=$\frac{1}{n}$AD,CD=nBE.
如图4,
DE=CE-CD=$\frac{1}{n}$AD-nBE;
如图5,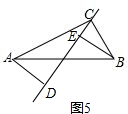
DE=CD-DE=nBE-$\frac{1}{n}$AD.
点评 本题是一道探究题,用到了全等三角形的判定与性质、相似三角形的判定与性质、三角形的内角和定理、平角的定义等知识,考查了探究能力,渗透了分类讨论的思想以及特殊到一般的思想,是一道好题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
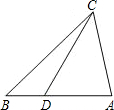 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )| A. | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=AD•AB |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
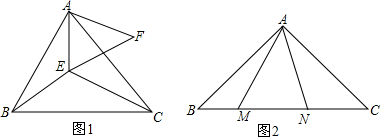
 如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.
如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.
如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com