
【题目】(1)如图1,已知AB∥CD,求证:∠EGF=∠AEG+∠CFG
(2)如图2,已知AB∥CD,∠AEF与∠CFE的平分线交于点G.猜想∠G的度数。证明你的猜想
(3)如图3,已知AB∥CD,EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,∠G=95°,求∠H的度数.
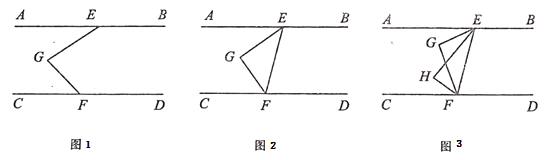
【答案】(1)见解析;(2)∠G=90°;证明见解析;(3)∠H=85°.
【解析】
(1)过点G作GH∥AB,根据两直线平行内错角相等可证得结论;
(2)由(1)得∠EGF=∠AEG+∠CFG,根据EG、FG分别平分∠AEF和∠CFE,得到∠AEF=2∠AEG,∠CFE=2∠CFG,由于AB∥CD得到∠AEF+∠CFE=180°,于是得到2∠AEG+2∠CFG=180°,即可得到结论;
(3)由(1)得∠G=∠AEG+∠CFG,∠H=∠AEH+∠CFH,根据EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,分别得到∠AEG=∠GEH=∠HEF=![]() ∠AEF,∠CFH=∠HFG=∠EFG=
∠AEF,∠CFH=∠HFG=∠EFG=![]() ∠CFE,结合∠AEF+∠CFE=180°,于是可求出∠CFE=105°,∠AEF=75°,代入∠H=
∠CFE,结合∠AEF+∠CFE=180°,于是可求出∠CFE=105°,∠AEF=75°,代入∠H=![]() ∠AEF+
∠AEF+![]() ∠CFE,计算即可得到结论.
∠CFE,计算即可得到结论.
解:(1)如图1,
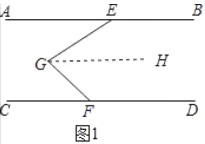
过点G作GH∥AB,
∴∠EGH=∠AEG.
∵AB∥CD,
∴GH∥CD.
∴∠FGH=∠CFG.
∴∠EGH+∠FGH=∠AEG+∠CFG.
即∠EGF=∠AEG+∠CFG;
(2)猜想:∠G=90°;
证明:如图2,
由(1)中的结论得:∠EGF=∠AEG+∠CFG,
∵EG、FG分别平分∠AEF和∠CFE,
∴∠AEF=2∠AEG,∠CFE=2∠CFG,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2∠AEG+2∠CFG=180°,
∴∠AEG+∠CFG=90°,
∴∠G=90°;
(3)解:如图3,
∵EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,
∴∠AEG=∠GEH=∠HEF=![]() ∠AEF,∠CFH=∠HFG=∠EFG=
∠AEF,∠CFH=∠HFG=∠EFG=![]() ∠CFE,
∠CFE,
由(1)可知,∠G=∠AEG+∠CFG,∠H=∠AEH+∠CFH,
∴∠G=![]() ∠AEF+
∠AEF+![]() ∠CFE=95°,
∠CFE=95°,
∴![]() (∠AEF+∠CFE)+
(∠AEF+∠CFE)+![]() ∠CFE=95°,
∠CFE=95°,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴∠CFE=105°,
∴∠AEF=75°,
∴∠H=![]() ∠AEF+
∠AEF+![]() ∠CFE=
∠CFE=![]() ×75°+
×75°+![]() ×105°=85°.
×105°=85°.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】已知,点P是等边△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若∠APB=150°,PA=9,PB=12,求PC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A型、B型、C型三种不同的纸板,其中A型:边长为a厘米的正方形;B型:长为a厘米,宽为1厘米的长方形;C型:边长为1厘米的正方形.
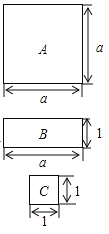
(1)A型2块,B型4块,C型4块,此时纸板的总面积为 平方厘米;
①从这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形,这个大正方形的边长为 厘米;
②从这10块纸板中拿掉2块同类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形,请问拿掉的是2块哪种类型的纸板?(计算说明)
(2)A型12块,B型12块,C型4块,从这28块纸板中拿掉1块纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出三个相同形状的大正方形,则大正方形的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,四边形ABCD是平行四边形,E,F是对角线AC上的两点,AE=CF.
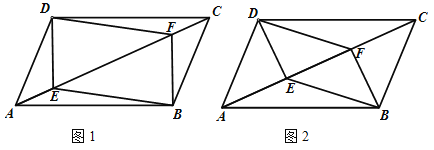
(1)求证:四边形DEBF是平行四边形;
(2)如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
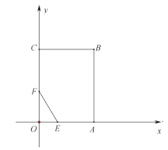
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴正半轴上,点
轴正半轴上,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,已知
,已知![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 从
从![]() 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线![]() 运动,设
运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
(3)在(2)的条件下,点![]() 为平面内一点,点
为平面内一点,点![]() 在线段
在线段![]() 上运动时,作
上运动时,作![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,
,![]() 为何值时,四边形
为何值时,四边形![]() 为矩形?并求此时点
为矩形?并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.

(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
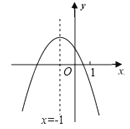
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润最多?最多获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度![]() ,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)

A. 33米 B. 34米 C. 35米 D. 36米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com