
 ��ͼ����֪A��2��0����B��1��m2-4m+5����
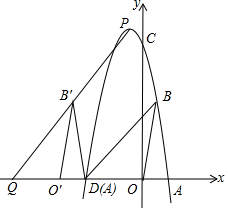
��ͼ����֪A��2��0����B��1��m2-4m+5�������� ��1����B��������֪��B���߶�OA�Ĵ�ֱƽ�����ϣ���֪OB=AB���ɵó��𰸣�
��2����m�ɱ�ʾ����ABO����������ö��κ��������ʿ������ȡ����Сֵʱ��m��ֵ��
��3���ٰ�B��������������߽���ʽ����m��ʾ��n��ֵ��������C��D�����ꣻ����B��D����ɱ�ʾ��ֱ��BD����ʽ����ƽ�ƿɱ�ʾ��B������꣬�Ӷ�����m��ʾ��ֱ��PQ�Ľ���ʽ������m��ʾ��P�����꣬����ֱ��PQ����ʽ����ɵõ�����m�ķ��̣������m��ֵ��
��� �⣺
��1����A��2��0����B��1��m2-4m+5����
���B���߶�OA�Ĵ�ֱƽ�����ϣ�
��OB=AB��
���ABO �ǵ��������Σ�
��2����S��ABO=$\frac{1}{2}$��2����m2-4m+5��=m2-4m+5=��m-2��2+1��
�൱m=2ʱ��S��ABO ����Сֵ��
��3���ٰ�B��1��m2-4m+5������
y=-��x-2����x-n����m2-4m+5=-��1-2����1-n����
��n=-��m-2��2��
��y=-x2+��-m2+4m-2��x+2��m-2��2��
��x=0����y=2��m-2��2��
��C��0��2��m-2��2����
��D��-��m-2��2��0����
�ڡ�B��1��m2-4m+5����D��-��m-2��2��0����
��ֱ��DB�Ľ���ʽΪy=x+��m-2��2��
��B'��-��m-2��2-1����m-2��2+1 ����
��ֱ��PQ�Ľ���ʽΪy=x+2��m-2��2+2��
�߶���P��$\frac{-��m-2��^{2}+2}{2}$��2��m-2��2+$\frac{[2-��m-2��^{2}]^{2}}{4}$����
��P����ֱ��PQ�ϣ�
��2��m-2��2+$\frac{[2-��m-2��^{2}]^{2}}{4}$��=$\frac{-��m-2��^{2}+2}{2}$+2��m-2��2+2��
��n=-��m-2��2��
��n2+2n-8=0
��n=-��m-2��2��
��n2+2n-8=0��
���n1=2��n2=-4��
��-��m-2��2=2����ȥ����m-2��2=4��
��m1=4��m2=0��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ�������߶δ�ֱƽ���ߵ��ж������ʡ����κ��������ʡ�����˼���֪ʶ���ڣ�1�����������ж�B���߶�OA�Ĵ�ֱƽ�������ǽ���Ĺؼ����ڣ�2������m��ʾ����ABO������ǽ���Ĺؼ����ڣ�3������m��ʾ�������ߺ�ֱ��PQ�Ľ���ʽ�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-1 | B�� | 2 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 3 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -1 | C�� | -$\frac{3}{2}$ | D�� | 0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com