
����Ŀ��[�������]
���ж�����������ȫ��ʱ��������һ��������ȫ���ж������⣬����"![]() " ����.���Ƶ�,���Ƕ�ֱ�����������Ƶ���������̽����
" ����.���Ƶ�,���Ƕ�ֱ�����������Ƶ���������̽����
(1) [�������]
������һ�������������ж��������⣬�������������"![]() "���ж�ֱ�����������Ƶķ�����������������Ϊ: .
"���ж�ֱ�����������Ƶķ�����������������Ϊ: .
(2) [����˼��]
���У����Dz����������÷������Ա�ʾΪ:��ͼ1,��![]() ��
��![]() ��
��![]() ,�� ,��
,�� ,��![]() �� �����֤��.
�� �����֤��.


(3) [�����о�]
��ͼ2�е�![]() ,�����������䣬�����������Ƿ�����?����������̽���Ľ��۽������,��������֤��,�������ƣ��뻭������.
,�����������䣬�����������Ƿ�����?����������̽���Ľ��۽������,��������֤��,�������ƣ��뻭������.
���𰸡�(1)�������ֱ�������ε�һ��ֱ�DZ���б�߶�Ӧ�ɱ����������������������ƣ�(2)![]() ��֤����������(3)����,֤��������.
��֤����������(3)����,֤��������.
��������
��1��������HL��ֱ�ӵó����ۣ�
��2���ȹ������A'C'B�ס�ACB�������жϳ�Rt��A'C'B��Rt��DFE���ɵó����ۣ�
��3���ȹ������AGC�ס�DHF��������2���Ľ��ۼ��ɵó����ۣ�
��1��б�ߺ�һ��ֱ�DZ߶�Ӧ�ɱ�������ֱ�����������ƣ�
�ʴ�Ϊ��б�ߺ�һ��ֱ�DZ߶�Ӧ�ɱ�������ֱ�����������ƣ�
��2����Rt��ABC��Rt��DEF�У���C=��F=90������![]() ������ABC�ס�DEF��
������ABC�ס�DEF��
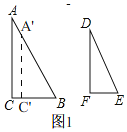
���ɣ���BA��ȡһ��A'ʹBA'=DE������A'��AC'��AC��BC��C'��
���A'C'B=��C=90��=��F����A'C'B�ס�ACB��
![]()
![]()
![]()
![]()
![]()
��Rt��A'C'B��Rt��DFE��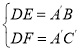 ��
��
��Rt��A'C'B��Rt��DFE��HL����
�ߡ�A'C'B�ס�ACB��
���DFE�ס�ACB��
�ʴ�Ϊ:![]() ��
��
��3����������ͼ2��
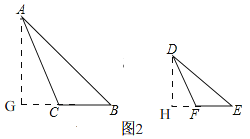
����A��AG��BC��BC���ӳ�����G������D��DH��EF��EF���ӳ�����H��
���G=��H=90����
�ߡ�ACB=��DFE��
���ACG=��DFH��
���AGC�ס�DHF��
���BAC=��FDH��
�ã�2���Ľ��۵ã���ABG�ס�DEH��
���B=��E����BAG=��EDH��
���BAC=��EDF��
�ߡ�B=��E��
���ABC�ס�DEF



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB��10CM���ҳ�AC��6cm����ACB��ƽ���߽���O�ڵ�D��
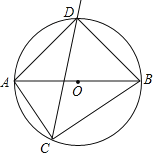
��1����BC�ij�.
��2������ABD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��ͼ��������������
��ͼ��������������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() ��ĺ�����Ϊ2.
��ĺ�����Ϊ2.

��1�����������ı��
��2��������![]() ���е�
���е�![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �ᴹֱ������Ϊ��
�ᴹֱ������Ϊ��![]() ��������������ͼ���ڵ�
��������������ͼ���ڵ�![]() ������
������![]() ��
��![]() �������
�������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
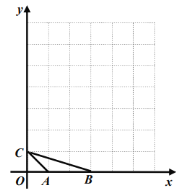
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ���������������ֱ�Ϊ��
���������������ֱ�Ϊ��![]() ��
��![]() ��
��![]() .
.
��1��![]() �����ԲԲ��
�����ԲԲ��![]() ������Ϊ .
������Ϊ .
��2�����Ե�![]() Ϊλ�����ģ������������ڻ���
Ϊλ�����ģ������������ڻ���![]() ��ʹ��
��ʹ��![]() ��
��![]() λ�ƣ��ҵ�
λ�ƣ��ҵ�![]() ���
���![]() ��Ӧ��λ�Ʊ�Ϊ2��1���ڵ�
��Ӧ��λ�Ʊ�Ϊ2��1���ڵ�![]() ����Ϊ .
����Ϊ .
��3��![]() �����Ϊ ��ƽ����λ.
�����Ϊ ��ƽ����λ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ�����������������У��١�AED����B����DE��BC����![]() ��
��![]() ����AD��BC��DE��AC���ݡ�ADE����C����������ADE����ACB��������( )
����AD��BC��DE��AC���ݡ�ADE����C����������ADE����ACB��������( )

A.1��B.2C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
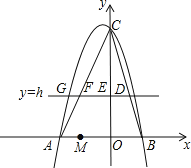
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx+6������A����3��0���͵�B��2��0����ֱ��y��h��hΪ��������0��h��6����BC���ڵ�D����y�ύ�ڵ�E����AC���ڵ�F��
��1���������ߵĽ���ʽ��
��2������AE����hΪ��ֵʱ����AEF��������
��3����֪һ����M����2��0�����ʣ��Ƿ����������ֱ��y��h��ʹ��BDM�ǵ��������Σ������ڣ������h��ֵ�͵�D�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾2017���ֵ2500��Ԫ��2019���ֵ3025��Ԫ
��1����2017����2019��ù�˾��ֵ����ƽ�������ʣ�
��2���ɣ�1�����ý����Ԥ��2020��ù�˾��ֵ���������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx+b�뷴��������y��![]() ��ͼ����A��2��3����B����3��n�����㣮
��ͼ����A��2��3����B����3��n�����㣮
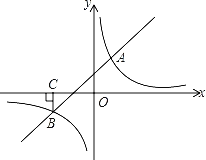
��1�����������Ľ���ʽ��
��2����B����BC��x�ᣬ����ΪC����P�Ƿ���������ͼ���ϵ�һ�㣬����PC��PB����PCB���������5ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר���꾭��ij���ͺŵ�������֪���ͺ������Ľ���Ϊ10��Ԫ/��������һ��ʱ����֣������ͺ������ۼ۶�Ϊ20��Ԫ/��ʱ��ƽ��ÿ���۳�8�����ۼ�ÿ����0.5��Ԫ��ƽ��ÿ�ܶ��۳�1��
��1����ÿ���������ۼ۽���x��Ԫ����ÿ�ܵ����������� �������ú�x�Ĵ���ʽ��ʾ��
��2�����õ�ƻ�ƽ��ÿ�ܵ�����������90��Ԫ��Ϊ�˾�����ٿ�棬�轫ÿ���������ۼ۽��Ͷ�����Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com