Question

4．已知：矩形ABCD内一点N，△ANB为等腰直角三角形，连结BN、CN并延长分别交DC，AD于点E，M，在AB上截取BF=EC，连接MF．
（1）求证：四边形FBCE为正方形；
（2）求证：MN=NC；
（3）若S_△FMC：S_{正方形FBCE}=2：3，求BN：MD的值．

Answer 1

分析 （1）先证明四边形FBCE为矩形，再利用△ANB为等腰直角三角形，证明△BEC为等腰直角三角形，则BC=CE，所以四边形FBCE为正方形；
（2）作辅助线，构建全等三角形，证明△BHN≌△AGN，得NG=NH，再利用平行线分线段成比例定理可得$\frac{MN}{NC}=\frac{NG}{NH}$=1，则MN=NC；
（3）设BF=1，表示出S_△FMC和S_{正方形FBCE}，并根据S_△FMC：S_{正方形FBCE}=2：3依次计算出FM、AM、MD、AB、BN的长，最后得结论．

解答 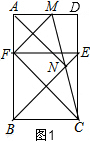解：（1）如图1，∵四边形ABCD为矩形，
∴AB∥CD，∠ABC=90°，
∴BF∥EC，
∵BF=EC，
∴四边形FBCE为矩形，
∵△ANB为等腰直角三角形，
∴∠ABE=45°，
∴∠EBC=45°，
∴△BEC为等腰直角三角形，
∴BC=CE，
∴四边形FBCE为正方形；
（2）如图2，过N作GH⊥BC，交BC于H，AD于G，则GH⊥AD，
∵AN=BN，∠AGH=∠BHG=90°，∠GAN=∠HBN=45°，
∴△BHN≌△AGN，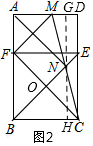
∴NG=NH，
∵AD∥BC，
∴$\frac{MN}{NC}=\frac{NG}{NH}$=1，
∴MN=NC；
（3）如图2，设FC与BE交于点O，设BF=1，则S_{正方形FBCE}=1，FC=$\sqrt{2}$，
∵FO=OC，MN=NC，
∴ON∥FM，
∴∠MFC=∠EOC=90°，
∴S_△MFC=$\frac{1}{2}$FC•FM=$\frac{\sqrt{2}}{2}$FM，
由于S_△FMC：S_{正方形FBCE}=2：3，即$\frac{\sqrt{2}}{2}$FM：1=2：3，
∴FM=$\frac{2\sqrt{2}}{3}$，
∵∠BFC=45°，∠MFC=90°，
∴∠AFM=45°，
∴△AFM是等腰直角三角形，
∴AF=AM=$\frac{2}{3}$，
∴MD=AD-AM=1-$\frac{2}{3}$=$\frac{1}{3}$，
AB=AF+BF=$\frac{2}{3}$+1=$\frac{5}{3}$，
∴cos45°=$\frac{BN}{AB}$，
∴BN=$\frac{\sqrt{2}}{2}$×$\frac{5}{3}$=$\frac{5\sqrt{2}}{6}$，
∴BN：MD=$\frac{5\sqrt{2}}{6}$：$\frac{1}{3}$=$\frac{5\sqrt{2}}{2}$．

点评 本题是四边形综合题，综合考查了矩形、正方形、等腰直角三角形及三角形中位线的性质，并利用特殊角的三角函数值求边的长；再计算边的比时，如果已知中没有说明任何一边的长度，可以设某一边为x或1进行计算．