
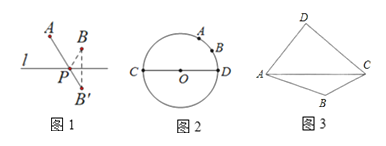
【题目】(理论学习)学习图形变换中的轴对称知识后,我们容易在直线![]() 上找到点
上找到点![]() ,使
,使![]() 的值最小,如图
的值最小,如图![]() 所示,根据这一理论知识解决下列问题:
所示,根据这一理论知识解决下列问题:
(1)(实践运用)如图![]() ,已知
,已知![]() 的直径
的直径![]() 为
为![]() ,弧
,弧![]() 所对圆心角的度数为
所对圆心角的度数为![]() ,点
,点![]() 是弧
是弧![]() 的中点,请你在直径
的中点,请你在直径![]() 上找一点
上找一点![]() ,使
,使![]() 的值最小,并求
的值最小,并求![]() 的最小值.
的最小值.
(2)(拓展延伸)在图![]() 中的四边形
中的四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(尺规作图,保留作图痕迹,不必写出作法).
.(尺规作图,保留作图痕迹,不必写出作法).
科目:初中数学 来源: 题型:
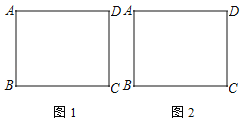
【题目】已知矩形ABCD,其中AD>AB,依题意先画出图形,然后解答问题.
(1)F为DC边上一点,把△ADF沿AF折叠,使点D恰好落在BC上的点E处.在图1中先画出点E,再画出点F,若AB=8,AD=10,直接写出EF的长为 ;
(2)把△ADC沿对角线AC折叠,点D落在点E处,在图2先画出点E,AE交CB于点F,连接BE.求证:△BEF是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
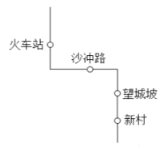
【题目】2018年12月1日,贵阳地铁一号线正式开通,标志着贵阳中心城区正式步入地铁时代,为市民的出行带来了便捷,如图是贵阳地铁一号线路图(部分),菁菁与琪琪随机从这几个站购票出发.
(1)菁菁正好选择沙冲路站出发的概率为
(2)用列表或画树状图的方法,求菁菁与琪琪出发的站恰好相邻的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .已知
.已知![]() ,抛物线的对称轴
,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求出![]() 的值;
的值;
(2)如图1,连接![]() ,点
,点![]() 是线段
是线段![]() 下方抛物线上的动点,连接
下方抛物线上的动点,连接![]() .点
.点![]() 分别在
分别在![]() 轴,对称轴
轴,对称轴![]() 上,且
上,且![]() 轴.连接
轴.连接![]() .当
.当![]() 的面积最大时,请求出点
的面积最大时,请求出点![]() 的坐标及此时
的坐标及此时![]() 的最小值;
的最小值;
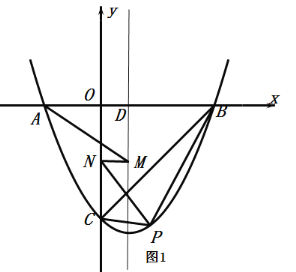
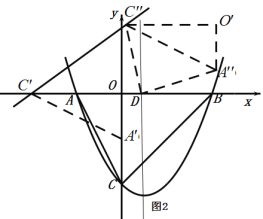
(3)如图2,连接![]() ,把
,把![]() 按照直线
按照直线![]() 对折,对折后的三角形记为
对折,对折后的三角形记为![]() ,把
,把![]() 沿着直线
沿着直线![]() 的方向平行移动,移动后三角形的记为
的方向平行移动,移动后三角形的记为![]() ,连接
,连接![]() ,
,![]() ,在移动过程中,是否存在
,在移动过程中,是否存在![]() 为等腰三角形的情形?若存在,直接写出点
为等腰三角形的情形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
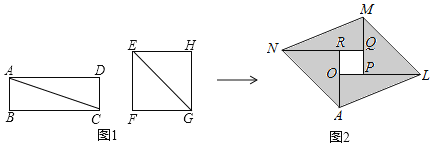
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
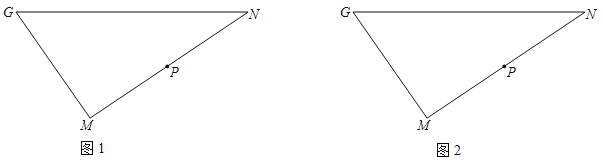
【题目】如图1,在Rt△GMN中,∠M=90°,P为MN的中点
(1)将线段MP绕着点M逆时针旋转60°得到线段MQ,点P的对应点为Q,若点Q刚好落在GN上,
①在图1中画出示意图;
②试问:以线段MQ为直径的圆是否与GN相切?请说明理由;
(2)如图2,用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN.(保留作图痕迹,不要求写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
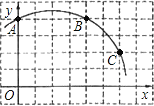
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及![]() 的长;
的长;
(3)有一点E(6,0),判断点E与⊙D的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c>0;④b﹣4a=0;⑤ 方程ax2+bx=0的两个根为 x1=0,x2=﹣4,其中正确的结论有( )
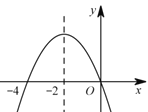
A.②③B.②③④C.②③⑤D.②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:

材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com