
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如![]() 表示5、3在数轴上对应的两点之间的距离;
表示5、3在数轴上对应的两点之间的距离; ![]() ,所以
,所以![]() 表示5、﹣3在数轴上对应的两点之间的距离;
表示5、﹣3在数轴上对应的两点之间的距离; ![]() ,所以
,所以![]() 表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为
表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为![]() .
.
问题(1):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(2):利用数轴探究:
①找出满足![]() 的x的所有值是 ,
的x的所有值是 ,
②设![]() ,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的取值范围是 时,
,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的取值范围是 时, ![]() 取得最小值,最小值是 .
取得最小值,最小值是 .
问题(3):求![]() 的最小值以及此时x的值;
的最小值以及此时x的值;
问题(4): ![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
![]()
【答案】(1) ![]() ;(2)①-2,4 ; ②4,0≤x≤2,2;(3)当x=2时,最小值为4;(4)-1≤x≤2,-2≤2y≤4,-3≤3z≤9 ,所以
;(2)①-2,4 ; ②4,0≤x≤2,2;(3)当x=2时,最小值为4;(4)-1≤x≤2,-2≤2y≤4,-3≤3z≤9 ,所以![]() 的最大值为15,最小值为-6.
的最大值为15,最小值为-6.
【解析】试题分析:(1)根据两点间的距离公式,可得答案;
(2)根据两点间的距离公式,点在线段上,可得最小值;
(3)![]() 根据问题(2)中的探究②可知,要使
根据问题(2)中的探究②可知,要使![]() 的值最小,
的值最小, ![]() 的值只要取-1到3之间(包括-1、3)的任意一个数,要使
的值只要取-1到3之间(包括-1、3)的任意一个数,要使![]() 的值最小,
的值最小, ![]() 应取2,显然当
应取2,显然当![]() 时能同时满足要求,把
时能同时满足要求,把![]() 代入原式计算即可;
代入原式计算即可;
(4)根据两点间的距离公式,点在线段上,可得答案.
试题解析:
问题(1)A到B的距离与A到C的距离之和可表示为|x+2|+|x1|;
问题(2)①2、4,
②4;不小于0且不大于2,2;
问题(3)由分析可知,
当x=2时能同时满足要求,把x=2代入原式=1+0+3=4;
![]()
![]()
所以![]() 的最大值为15,最小值为-6.
的最大值为15,最小值为-6.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.对角线相等且互相垂直的四边形是正方形.
B.坡面的水平宽度与铅直高度的比称为坡度.
C.两个相似图形也是位似图形.
D.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点. 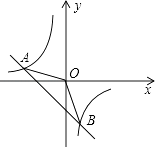
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△ABO的面积;
(3)根据图象直接写出当一次函数的值大于反比例函数的值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
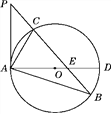
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某楼盘2018年初房价为每平方米20000元,经过两年连续降价后,2020 年初房价为16200元。设该楼盘这两年房价年平均降低的百分率为x,根据题意可列方程为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com