练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．两车站相距175千米，慢车以每小时50千米的速度从甲站开往乙站，1小时后，快车以每小时75千米的速度从乙站开往甲站，那么慢车开出几小时后与快车相遇？

    分析 设慢车开出x小时后与快车相遇，则快车行驶了（x-1）小时，根据两地之间的距离=慢车速度×慢车行驶时间+快车速度×快车行驶时间，即可得出关于x的一元一次方程，解之即可得出结论．

    解答 解：设慢车开出x小时后与快车相遇，则快车行驶了（x-1）小时，
    根据题意得：50x+75（x-1）=175，
    解得：x=2．
    答：慢车开出2小时后与快车相遇．

    点评 本题考查了一元一次方程的应用，根据两地之间的距离=慢车速度×慢车行驶时间+快车速度×快车行驶时间，列出关于x的一元一次方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

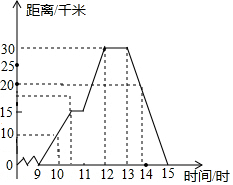    14．如图表示一人骑自行车离家的距离与时间的关系，骑车者9时离开家，15时到家，根据图象回答问题：
    （1）到达离家最远的地方是什么时间？离家多远？
    （2）第一次休息时离家多远？
    （3）返回时的平均速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

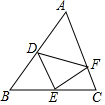    15．如图，设△ABC的面积为1，点D，E，F分别在AB，BC，CA上，AD=$\frac{1}{m}$AB，BE=$\frac{1}{n}$BC，CF=$\frac{1}{p}$CA，且满足m+n+p=9，m2+n2+p2=29．m3+n3+p3=99，求△DEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知：△ABC∽△A′B′C′，下列图形中，△ABC与△A′B′C′不存在位似关系的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．计算：2$\frac{1}{3}$-（-$\frac{1}{3}$）=2$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．将直线y=3x向下平移3个单位，所得到的直线的函数关系式是y=3x-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

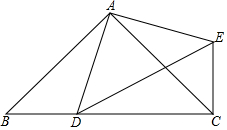    16．填空：把下面的推里过程补充完整，并在括号内注明理由．
    如图，已知：△ABC与△ADE均是等腰直角三角形，∠BAC=∠DAE=90°，D在BC上．
    求证：BD=CE．
    证明：∵△ABC与△ADE均是等腰直角三角形（已知）
    ∴AB=AC
    AD=AE（等腰直角三角形两腰相等）
    ∵∠BAC=∠DAE=90°（已知）
    ∠BAC=∠BAD+∠DAC，∠DAE=∠CAE+∠DAC
    ∴∠BAD=∠CAE（同角的余角相等）
    ∴△ABD≌△ACE（SAS）
    ∴BD=CE（全等三角形的对应边相等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．8056000用科学记数法表示是8.056×106．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如果将一个小球放在如图所示的地板上自由滚动，小球随机地停留在某块方砖上，那么它停留在黑色区域的概率是$\frac{2}{9}$．

    查看答案和解析>>

    同步练习册答案