
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 经过点
经过点![]() 和
和![]() .
.
(1)求该抛物线的解析式及顶点坐标;
(2)把该抛物线向 (填“上”或“下”)平移 个单位长度,得到的抛物线与![]() 轴只有一个公共点;
轴只有一个公共点;
(3)平移该抛物线,使平移后的抛物线经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,同时满足以
,同时满足以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
【答案】(1)抛物线的解析式为![]() ,顶点坐标为
,顶点坐标为![]() ;(2)下,
;(2)下,![]() ;(3)将原抛物线向左平移3个单位,再向下平移3个单位或将原抛物线先向左平移2个单位,再向下平移5个单位,理由见解析.
;(3)将原抛物线向左平移3个单位,再向下平移3个单位或将原抛物线先向左平移2个单位,再向下平移5个单位,理由见解析.
【解析】
(1)将点![]() 和
和![]() 代入抛物线解析式可求出a,b,进而得到抛物线解析式,将解析式化成顶点式可得顶点坐标;
代入抛物线解析式可求出a,b,进而得到抛物线解析式,将解析式化成顶点式可得顶点坐标;
(2)根据平移规律进行解答;
(3)根据![]() 是等腰直角三角形可得点
是等腰直角三角形可得点![]() 的坐标为
的坐标为![]() 或
或![]() ,分情况讨论,分别求出抛物线解析式,进而判断平移方式即可.
,分情况讨论,分别求出抛物线解析式,进而判断平移方式即可.
解:(1)由题意,得![]() ,
,
解得![]() ,
,
∴该抛物线的解析式为![]() ,
,
∵![]()
![]() ,
,
∴顶点坐标为![]() ;
;
(2)∵当顶点坐标为![]() 时,抛物线与
时,抛物线与![]() 轴只有一个公共点,
轴只有一个公共点,
∴需要把该抛物线向下平移![]() 个单位长度;
个单位长度;
(3)![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 在
在![]() 轴上,
轴上,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() ,
,
设平移后的抛物线的解析式为![]() ,
,
①当抛物线过点![]() ,
,![]() 时,有
时,有![]() ,
,
解得![]() ,
,
![]() 平移后的抛物线的解析式
平移后的抛物线的解析式![]() ,
,
![]() 该抛物线的顶点坐标为
该抛物线的顶点坐标为![]() ,
,
![]() 原抛物线的顶点坐标为
原抛物线的顶点坐标为![]() ,
,
![]() 将原抛物线向左平移3个单位,再向下平移3个单位即可得到符合条件的抛物线;
将原抛物线向左平移3个单位,再向下平移3个单位即可得到符合条件的抛物线;
②当抛物线过![]() ,
,![]() 时,有
时,有![]() ,
,
解得![]() ,
,
![]() 平移后的抛物线的解析式为
平移后的抛物线的解析式为![]() ,
,
![]() 该抛物线的顶点坐标为
该抛物线的顶点坐标为![]() ,
,
![]() 原抛物线的顶点坐标为
原抛物线的顶点坐标为![]() ,
,
![]() 将原抛物线先向左平移2个单位,再向下平移5个单位即可得到符合条件的抛物线.
将原抛物线先向左平移2个单位,再向下平移5个单位即可得到符合条件的抛物线.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=72°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为

A. 36° B. 40° C. 45° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,若BC是Rt△ABC和Rt△DBC的公共斜边,则A、B、C、D在以BC为直径的圆上,则叫它们“四点共圆”.如图②,△ABC的三条高AD、BE、CF相交于点H,则图②中“四点共圆”的组数为( )
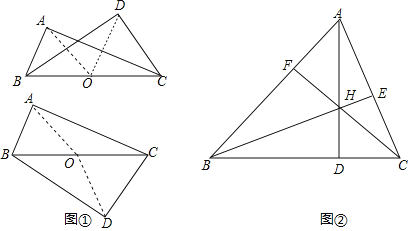
A.2B.3C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 与
与![]() ,下列判断不正确的是( )
,下列判断不正确的是( )
A.若方程![]() 有两个实数根,则方程
有两个实数根,则方程![]() 也有两个实数根;
也有两个实数根;
B.如果![]() 是方程
是方程![]() 的一个根,那么
的一个根,那么![]() 是
是![]() 的一个根;
的一个根;
C.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1;
有一个根相等,那么这个根是1;
D.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1或-1.
有一个根相等,那么这个根是1或-1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=![]() (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(1)求点D的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.
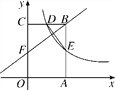
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润.

(1)求小琴的父母今年共收获金溪密梨多少斤?
(2)若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD和正方形AEFG中,点B在边AG上,点D在线段EA的延长线上,连接BE.
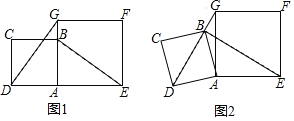
(1)如图1,求证:DG⊥BE;
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,使点B恰好落在线段DG上.
①求证:DG⊥BE;
②若AB=2,AG=3,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com