
分析 (1)设乙每小时加工x个零件,则甲每小时加工(x+8)个零件,根据甲、乙完成任务的时间比是4:5列出方程解答即可;
(2)根据$\frac{480}{x+8}-\frac{400}{x}$的值大于零,等于零,小于零三种情形考虑即可得出结论.
解答 解:(1)设乙每小时加工x个零件,则甲每小时加工(x+8)个零件,由题意得
$\frac{480}{x+8}$=$\frac{400}{x}$×$\frac{4}{5}$
解得:x=16
经检验x=16是原分式方程的解,
答:乙每小时加工16个零件.
(2)设乙每小时加工x个零件,则甲每小时加工(x+8)个零件,
∵$\frac{480}{x+8}-\frac{400}{x}$=$\frac{480x-400x-3200}{x(x+8)}$=$\frac{80x-3200}{x(x+8)}$,
当80x-3200>0时,x>40,
当80x-3200=0时,x=40,
当80x-3200<0时,x<40,
又∵x≥20,
∴20≤x<40时,甲先完成任务.
x=40时,甲、乙工作时间相同.
x>40时,乙先完成任务.
点评 本题考查分式方程的应用、一元一次不等式的应用,找到等量关系或不等量关系是解决问题的关键,解分式方程注意检验.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
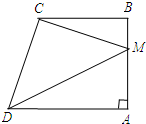 如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.
如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
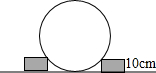 某公园中央地上有一个大理石球,小明想测量球的半径.于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,聪明的你也能算出这个大石球的半径了吗?写出你的计算过程.
某公园中央地上有一个大理石球,小明想测量球的半径.于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,聪明的你也能算出这个大石球的半径了吗?写出你的计算过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,折线ABCDE描述汽车在某一直线公路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
如图,折线ABCDE描述汽车在某一直线公路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:| A. | ① | B. | ② | C. | ③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
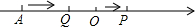 如图,在数轴上点A对应的数为-6,点P从原点O出发以每秒1个单位长度的速度向正方向运动,同时,点Q从点A出发以每秒2个单位长度的速度向正方向运动,则经过$\frac{12}{7}$或12秒钟,OQ=$\frac{3}{2}$OP.
如图,在数轴上点A对应的数为-6,点P从原点O出发以每秒1个单位长度的速度向正方向运动,同时,点Q从点A出发以每秒2个单位长度的速度向正方向运动,则经过$\frac{12}{7}$或12秒钟,OQ=$\frac{3}{2}$OP.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com