
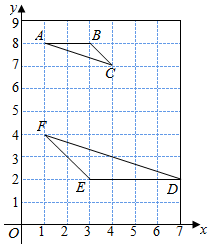
 ��ͼ����ƽ��ֱ������ϵ�У�ÿ��С�����DZ߳�Ϊ1����λ��С�����Σ���A��B��C���Ǹ�㣨ÿ��С����Ķ���и�㣩������A��1��8����B��3��8����C��4��7����
��ͼ����ƽ��ֱ������ϵ�У�ÿ��С�����DZ߳�Ϊ1����λ��С�����Σ���A��B��C���Ǹ�㣨ÿ��С����Ķ���и�㣩������A��1��8����B��3��8����C��4��7�������� ��1���������ҵĶ��壬��������ص���
��2�������߶δ�ֱƽ���ߵ����ʺ������ε����Բ�ĸ�����
��3������λ�Ʊ任��λ�����ĵĸ�����
��4���������������εĶ�Ӧ�ߵı���ȣ����������ƱȽ��
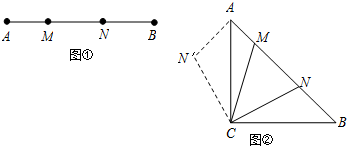
��� 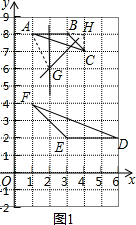 �⣺��1����ͼ1���������ص���ɶ����ã�CH=1��AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
�⣺��1����ͼ1���������ص���ɶ����ã�CH=1��AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
��sinA=$\frac{HC}{AC}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$��
�ʴ�Ϊ��$\frac{\sqrt{10}}{10}$��
��2����AB��BC�Ĵ�ֱƽ���߽���G������AG��
���������ص��֪����G������Ϊ��2��6����
��AG=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��
���ABC���Բ�İ뾶��$\sqrt{5}$��
�ʴ�Ϊ��$\sqrt{5}$��
��3����ͼ2������BE��FC��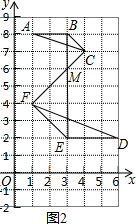 ���������ص㣬BE��FC���ڵ�M��
���������ص㣬BE��FC���ڵ�M��
��M��������3��6����
����λ�����ĵĸ����֪��λ������M�������ǣ�3��6����
�ʴ�Ϊ����3��6����
��4���������ص��֪��AB=2��BC=$\sqrt{2}$��AC=$\sqrt{10}$��
�ߡ�A1B1C1�ס�ABC�������Ʊ�Ϊ$\sqrt{2}$��1
��A1B1=2$\sqrt{2}$��B1C1=2��A1C1=2$\sqrt{5}$��
����ġ�A1B1C1��ͼ3��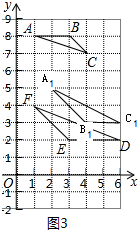
���� ���⿼����Ǹ�������Ρ�������Ǻ����Ķ��塢λ�Ʊ任��λ�����������������ε����ʣ������������ͼ�β���������ͼ�Σ��Ҷ�Ӧ�������ཻ��һ�㣬��Ӧ�߶λ���ƽ�У�������ͼ����λ��ͼ���ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��Уһ��Χǽ����������̨���棬��ͼ��Ӱ������ʾ����̨������̨�߶���ȣ�������ͬ����Ҫ�øֹ�����������ACG��������ˮƽ����PQ��ֱ�Ļ���֧��CD��EF��GH����D��F��H�ֱ���ÿ��̨���е㴦������֪��̨��Ϊ1.2�ף�����֧��CD=GH=0.8�ף���DCG=66.5�㣮���ο����ݣ�sin66.5��=0.92��cos66.5��=0.40��tan66.5��=2.30��
��Уһ��Χǽ����������̨���棬��ͼ��Ӱ������ʾ����̨������̨�߶���ȣ�������ͬ����Ҫ�øֹ�����������ACG��������ˮƽ����PQ��ֱ�Ļ���֧��CD��EF��GH����D��F��H�ֱ���ÿ��̨���е㴦������֪��̨��Ϊ1.2�ף�����֧��CD=GH=0.8�ף���DCG=66.5�㣮���ο����ݣ�sin66.5��=0.92��cos66.5��=0.40��tan66.5��=2.30���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
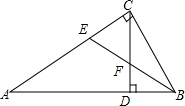 ��ͼ����֪��ABC�У���ACB=90�㣬CDΪAB���ϵĸߣ���ABC��ƽ����BE�ֱ�CD��CA�ڵ�F��E�������н�����ȷ���У�������
��ͼ����֪��ABC�У���ACB=90�㣬CDΪAB���ϵĸߣ���ABC��ƽ����BE�ֱ�CD��CA�ڵ�F��E�������н�����ȷ���У�������| A�� | �٢ۢ� | B�� | �ڢۢ� | C�� | �٢ڢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-$\frac{1}{2}+$x+$\frac{1}{x}$ | B�� | y=1+x+5x2 | C�� | y=22+2x | D�� | y=$\frac{1}{2}{x}^{3}-{x}^{2}+25$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com