
【题目】如图,已知:梯形ABCD中,∠ABC=90°,∠DAB=45°,AB∥DC,DC=3,AB=5,点P在AB边上,以点A为圆心AP为半径作弧交边DC于点E,射线EP于射线CB交于点F.

(1)若AP![]() ,求DE的长;
,求DE的长;
(2)联结CP,若CP=EP,求AP的长;
(3)线段CF上是否存在点G,使得△ADE与△FGE相似?若相似,求FG的值;若不相似,请说明理由.
【答案】(1)1;(2)AP![]() ;(3)FG=3
;(3)FG=3![]() 1.
1.
【解析】
(1)如图,过点A,作AH//BC,交CD的延长线于点H,在Rt△AHE中求出AE,即可求解;
(2)设:AP=x,利用△APE∽△PEC,得出PC2=CEAP,利用勾股定理得出PC2=PB2+BC2,即可求解;
(3)利用△ADE∽△FGE,得到3α=45°,进而求出相应线段的长度,再利相似比![]() ,即可求解.
,即可求解.
解:(1)如图1中,过点A,作AH∥BC,交CD的延长线于点H.

∵AB∥CD,
∴∠ABC+∠C=180°,
∵∠ABC=90°,
∴∠C=∠ABC=∠H=90°,
∴四边形AHCB是矩形,
∴AB=CH=5,∵CD=3,
∴DH=CH﹣CD=2,
∵∠HAB=90°,∠DAB=45°,
∴∠HAD=∠HDA=45°
∴HD=AH=2,AE=AP![]() ,
,
根据勾股定理得,HE![]() 3,则ED=1;
3,则ED=1;
(2)连接CP,设AP=x.

∵AB∥CD,
∴∠EPA=∠CEP,即等腰△APE、等腰△PEC两个底角相等,
∴△APE∽△PEC,∴![]() ,
,
即:PE2=AECE,
而EC=2PB=2(5﹣x),
即:PC2=CEAP=2(5﹣x)x,
而PC2=PB2+BC2,即:PC2=(5﹣x)2+22,
∴2(5﹣x)x=(5﹣x)2+22,
解得:x![]() (不合题意值已舍去),
(不合题意值已舍去),
即:AP![]() ;
;
(3)如图3中,在线段CF上取一点G,连接EG.

设∠F=α,则∠APE=∠AEP=∠BPF=90°﹣α,
则:∠EAP=180°﹣2∠APE=2α,
∵△ADE∽△FGE,设∠DAE=∠F=α,
由∠DAB=45°,可得3α=45°,2α=30°,
在Rt△ADH中,AH=DH=2,
在Rt△AHE中,∠HEA=∠EAB=2α=30°,∠HAE=60°,
∴HE=AHtan∠HAE=2![]() ,
,
∴DE=HE﹣HD=2![]() 2,
2,
EC=HC﹣HE=5﹣2![]() ,
,
∵△ADE∽△FGE,
∴∠ADC=∠EGF=135°,
则∠CEG=45°,
∴EG![]() EC=5
EC=5![]() 2
2![]() ,
,
∴![]() ,
,
即:![]() ,
,
解得:FG=3![]() 1.
1.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】(探究与创新):已知A、B在数轴上分别表示a、b
①对照数轴填写下表:
a | 6 | ﹣6 | ﹣6 | 2 | ﹣1.5 |
b | 4 | 0 | ﹣4 | ﹣10 | ﹣1.5 |
A、B两点的距离 | 2 |
|
|
| 0 |
②若A、B两点间的距离记为d,则d和a、b之间有何数量关系?(直接写出结果)
③在数轴上标出所有符合条件的整数点P使它到5和﹣5的距离之和为10,并求出所有这些整数的和.
![]()
④若点Q表示的数为x,当点Q在什么位置时,|x+1|+|x﹣2|有最小值?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,电脑绣花设计师准备在长120cm,宽8cm的矩形ABCD模板区域内设计绣花方案,现将其划分为区域Ⅰ(2个全等的五边形),区域Ⅱ(2个全等的菱形),区域Ⅲ(正方形EFGH中减去与2个菱形重合的部分),剩余为不刺绣的空白部分:点O是整副图形的对称中心EG∥AB,H,F分别为2个菱形的中心,MH=2PH,HQ=2OQ,为了美观,要求MT不超过10cm.若设OQ=x(cm),x为正整数.

(1)用含x的代数式表示区域Ⅲ的面积;
(2)当矩形ABCD内区域Ⅰ的面积最小时,图案给人的视觉感最好.求此时MN的长度;
(3)区域Ⅰ,Ⅱ,Ⅲ的刺绣方式各有不同.区域Ⅰ与区域Ⅲ所用的总针数之比为29:19,区域Ⅱ与区域Ⅲ每平方厘米所用的针数分别为a,b针(a,b均为整数,a>b),区域Ⅲ的面积为正整数.这时整个模板的总针数为12960针,则a+b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
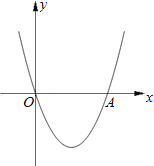
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
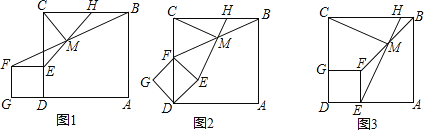
【题目】如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系;
(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
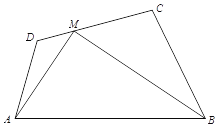
【题目】如果从一个四边形一边上的点到对边的视角是直角,那么称该点为直角点.例如,如图的四边形ABCD中,点![]() 在边CD上,连结
在边CD上,连结![]() 、
、![]() ,
,![]() ,则点
,则点![]() 为直角点.若点
为直角点.若点![]() 、
、![]() 分别为矩形ABCD边
分别为矩形ABCD边![]() 、CD上的直角点,且
、CD上的直角点,且![]() ,
,![]() ,则线段
,则线段![]() 的长为____.
的长为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com