【题目】已知，如图，在△
中，
分别是△的高和角平分线，若
,
;求
的度数.
【答案】
【解析】
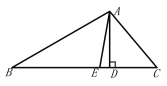
根据三角形内角和定理得到∠BAC+∠B+∠C=180°，而∠B=30°，∠C=50°，可求得∠BAC=180°-30°-50°=100°，根据△ABC的角平分线的定义得到∠EAC=
∠BAC=50°，而AD为△
的高，则∠ADC=90°，而∠C=50°，于是∠DAC=180°-90°-50°=40°，然后利用∠DAE=∠EAC-∠DAC计算即可．
∵∠BAC+∠B+∠C=180°，
而∠B=30°,∠C=50°，
∴∠BAC=180°30°50°=100°，
∵AE是△ABC的角平分线，
∴∠EAC=∠BAC=50°，
又∵AD为△ABC的高，
∴∠ADC=90°，
而∠C=50°，
∴∠DAC=180°90°50°=40°，
∴∠DAE=∠EAC∠DAC=50°40°=10°.
故答案为10°.
科目：初中数学 来源： 题型：
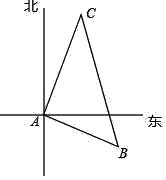
【题目】如图，有一艘货船和一艘客船同时从港口A出发，客船每小时比货船多走5海里，客船与货船速度的比为4：3，货船沿东偏南10°方向航行，2小时后货船到达B处，客船到达C处，若此时两船相距50海里．
（1）求两船的速度分别是多少？
（2）求客船航行的方向．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在梯形ABCD中，AD∥BC，BC=2AD，点F、G分别是边BC、CD的中点，连接AF、FG，过点D作DE∥FG交AF于点E．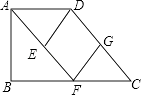 
（1）求证：△AED≌△CGF；
（2）若梯形ABCD为直角梯形，∠B=90°，判断四边形DEFG是什么特殊四边形？并证明你的结论；
（3）若梯形ABCD的面积为a（平方单位），则四边形DEFG的面积为（平方单位）．（只写结果，不必说理）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）拼一拼，画一画：请你用4个长为a，宽为b的矩形拼成一个大正方形，并且正中间留下一个洞，这个洞恰好是一个小正方形。
（2）用不同方法计算中间的小正方形的面积，聪明的你能发现什么？
（3）当拼成的这个大正方形边长比中间小正方形边长多3cm时，它的面积就多24cm2，求中间小正方形的边长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知双曲线y=
（k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣8，4），则△AOC的面积为（ ）
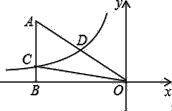
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
科目：初中数学 来源： 题型：
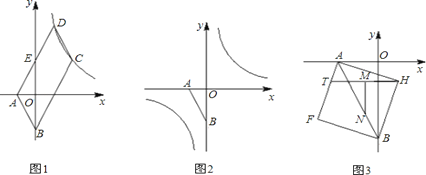
【题目】如图1，已知点A（a，0），B（0，b），且a、b满足
=0， □ABCD的边AD与y轴交于点E(0，2)，且E为AD中点，双曲线
经过C、D两点．
（1）求k的值；
（2）点P在双曲线上，点Q在y轴上，若以点A、B、P、Q为顶点的四边形是平行四边形，试求满足要求的所有点P、Q的坐标；
（3）以线段AB为对角线作正方形AFBH（如图3），点T是边AF上一动点，M是HT的中点，MN⊥HT，交AB于N，当T在AF上运动时，
的值是否发生改变？若改变，求出其变化范围；若不改变，请求出其值，并给出你的证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
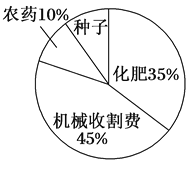
【题目】某地农民一直保持着冬种油菜的习惯，利用农闲冬种一季油菜．该地农业部门对2017年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计，并绘制了如下的统计表与统计图(如图)：
每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
110元 | 130千克 | 3元/千克 | 500 000亩 |
请根据以上信息解答下列问题：
(1)种植油菜每亩的种子成本是多少元？
(2)农民冬种油菜每亩获利多少元？
(3)2017年该地全县农民冬种油菜的总获利是多少元？(结果用科学记数法表示)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AC=BC，∠ACB=90°，点D、E在AB上，将△ACD、△BCE分别沿CD、CE翻折，点A、B分别落在点A′、B′的位置，再将△A′CD、△B′CE分别沿A′C、B′C翻折，点D与点E恰好重合于点O，则∠A′OB′的度数是_________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
