练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．用科学记数法表示525 000正确的是（　　）
    A．5.25×106B．5.25×105C．5.25×104D．525×103

    分析 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

    解答 解：将525000用科学记数法表示为：5.25×105．
    故选B．

    点评 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．若以两根4cm，9cm的木棒为边做一个等腰三角形，还需要选用一根9cm长的木棒．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．某企业五月份的利润是25万元，预计七月份利润将增加11万元，则六、七月份的平均增长率是20%．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

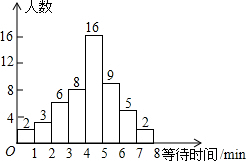    17．超市为了制定某个时间段收银台开放方案，统计了这个时间段本超市收银台排队付款的等待时间，并绘制成如图所示的频数分布直方图（图中等待时间0分钟到1分钟表示大于或等于0分钟而小于1分钟，其他类同）．这个时间段内顾客等待时间不少于6分钟的人数为7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，在△ABC中，∠C=90°，AB=1，∠A=α，则cosα=$\frac{AC}{AB}$=AC．现在将△ABC沿AC折叠，得到△ADC，如图2，易知B，C，D三点共线，∠DAB=2α（其中0°＜α＜45°）．
    过点D作DE⊥AB于点E，
    ∵∠DCA=∠DEA=90°，∠DFC=∠AFE，
    ∴∠BDE=∠BAC=α，
    ∵BD=2BC=2sinα，
    ∴BE=BD•sinα=2sinα．sinα=2sin2α，
    ∴AE=AB-BE=l-2sin2α，
    ∴∴cos2α=cos∠DAE=$\frac{AE}{AD}$=$\frac{1-2si{n}^{2}α}{1}$=1-sin2α
    阅读以上内容，回答下列问题：
    （1）如图1，若BC=$\frac{1}{3}$，则cosα=$\frac{2\sqrt{2}}{3}$，cos2α=$\frac{7}{9}$；
    （2）求出sin2α的表达式（用含sinα或cosα的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，AB是⊙O的一条弦，OD⊥AB于点C，交⊙O于点D，点E在⊙O上，∠AED=30°，OB=10，则弦AB=10$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知函数y=x2+2ax+1在-1≤x≤2上的最大值为4，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知某汽车的油箱最多能装油80升，一天小明加满油后打算从A地到400千米的B地接人，接到人后按原路返回，请回答下列问题：油箱注满油后，汽车能够行使的总路程a（单位：千米）与每千米平均耗油量b（单位：升）之间有怎样的函数关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

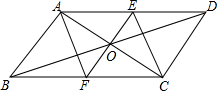    8．如图：在平行四边形ABCD中，对角线AC与BD交于点O，过点O的直线EF分别与AD、BC交于点E、F，EF⊥AC，连结AF、CE．
    （1）求证：OE=OF；
    （2）请判断四边形AECF是什么特殊四边形，请证明你的结论．

    查看答案和解析>>

    同步练习册答案