
���� ������������Ĺ��ɼ�����⣮
��� �⣺��1����1+2+3+4+5��2=225
��2��ԭʽ=[$\frac{1}{2}$n��n+1��]2=$\frac{1}{4}$n2��n+1��2
��3����ԭʽ=��3��1��3+��3��2��3+��3��3��3+��+��3��20��3
=27��13+27��23+27��33+��+27��203
=27��13+23+33+��+203��
=27��$\frac{1}{4}$��202��212
=27��44100
=1190700
��ԭʽ=[13+23+33+��+��2n��3]-[23+43+63+��+��2n��3]
=$\frac{1}{4}$��2n��2��2n+1��2-8��13+23+33��+n3��
=$\frac{1}{4}$��4n2��2n+1��2-8��$\frac{1}{4}$��n2����n+1��2
=n2��2n+1��2-2n2��n+1��2
=n2��2n2-1��
=2n4-n2
��4���ߣ�n+1��3=n3+3n2+3n+1
�ࣨn+1��3-n3=3n2+3n+1
��n3-��n-1��3=3��n-1��2+3��n-1��+1
��
��33-23=3��22+3��2+1��
��23-13=3��12+3��1+1
����n����ʽ��ӣ���
��n+1��3-13=3��12+22+��+n2��+3��1+2+��+n��+n
��3��12+22+��+n2��=��n+1��3-1-3��1+2+��+n��-n
=��n+1��3-3��$\frac{n��n+1��}{2}$-��n+1��
=��n+1��[��n+1��2-$\frac{3}{2}$n-1]
=��n+1����n2+$\frac{1}{2}$n��
��12+22+��+n2=$\frac{1}{6}$n��n+1����2n+1��
�ߣ�n+1��4=n4+4n3+6n2+4n+1��
�ࣨn+1��4-n4=4n3+6n2+4n+1��
��n4-��n-1��4=4��n-1��3+6��n-1��2+4��n-1��+1��
��
34-24=4��23+6��22+4��2+1
24-14=4��13+6��12+4��1+1
����n����ʽ��ӣ���
��n+1��4-n4=4��13+23+��+n3��+6��12+22+��+n2��+4��1+2+��+n��+n��
��4��13+23+��+n3��=��n+1��4-1-6��12+22+��+n2��-4��1+2+��+n��-n
=��n+1��4-6��$\frac{1}{6}$n��n+1����2n+1��-4��$\frac{n��n+1��}{2}$-��n+1��
=��n+1��[��n+1��3-n��2n+1��-2n-1]
=��n+1����n3+n2��
��13+23+��+n3=$\frac{1}{4}$n2��n+1��2
�ʴ�Ϊ��1��225����2��$\frac{1}{4}$n2��n+1��2
���� ���⿼����ʽ�ֽ��Լ����ֹ��ɣ��漰��ʽ������㣬�����������֪ʶ���ۺϳ̶Ƚϸߣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
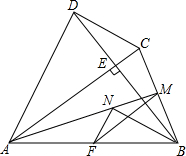 ��ͼ���ı���ABCD�У�AC��BD��BD�ڵ�E����F��M�ֱ���AB��BC���е㣬BNƽ�֡�ABE��AM�ڵ�N��AB=AC=BD������MF��NF����˵����
��ͼ���ı���ABCD�У�AC��BD��BD�ڵ�E����F��M�ֱ���AB��BC���е㣬BNƽ�֡�ABE��AM�ڵ�N��AB=AC=BD������MF��NF����˵�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com