
已知:在平面直角坐标系xOy中,给出如下定义:线段AB及点P,任取AB上一点Q,线段PQ长度的最小值称为点P到线段AB的距离,记作d(P→AB).
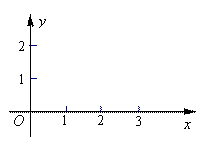
(1)如图1,已知C点的坐标为(1,0),D点的坐标为(3,0),求点P(2,1)到线段CD的距离d(P→CD)为  ;
;
 (2)已知:线段EF:y=x(0≤x≤3),点G到线段EF的距离d(P→EF)为
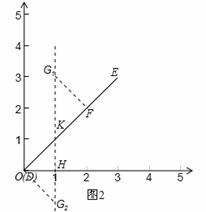
(2)已知:线段EF:y=x(0≤x≤3),点G到线段EF的距离d(P→EF)为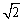 ,且点G的横坐标为1,在图2中画出图,试求点G的纵坐标.
,且点G的横坐标为1,在图2中画出图,试求点G的纵坐标.
图1 图2
(1) d(P→CD)为 1
(2)在坐标平面内作出线段DE:y=x(0≤x≤3).
∵点G的横坐标为1,
∴点G在直线x=1上,设直线x=1交x轴于点H,交DE于点K,
①如图2所示,过点G1作G1F⊥DE于点F,则G1F就是点G1到线段DE的距离,
∵线段DE:y=x(0≤x≤3),
∴△G1FK,△DHK均为等腰直角三角形,
∵G1F=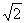
∴KF=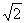
由 勾股定理得G1K=2,
勾股定理得G1K=2,
又∵KH=OH=1,
∴H G1=3,即G1的纵坐标为3;
G1=3,即G1的纵坐标为3;
②如图2所示,过点O作G2O⊥OE交直线x=1于点G2,由题意知△OHG2为等腰直角三角形,
∵OH=1,
∴G2O=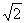
∴点G2同样是满足条件的点,
∴点G2的纵坐标为-1,
综上,点G的纵坐标为3或-1.
 |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
 (1)求证:DE与⊙O 相切.
(1)求证:DE与⊙O 相切.
(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
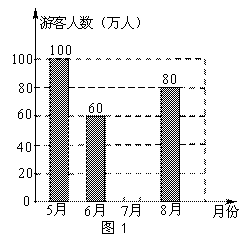
以下是根据2013年某旅游县接待游客的相关数据绘制的统计图的一部分,请根据图1,图2回答下列问题:
(1)该旅游县5~8月接待游客人数一共是280万人,请将图1中的统计图补充完整;
(2)该旅游县6月份4A级景点接待游客人数约为多少人?
(3)小明观察图2后认为,4A级景点7月份接待游客人数比8月多了,你同意他的看
|
|
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系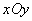 中,已知直线l:
中,已知直线l: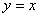 ,作
,作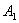 (1,0)关于
(1,0)关于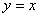 的对称点
的对称点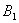 ,将点
,将点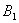 向右水平平移2个单位得到点
向右水平平移2个单位得到点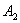 ;再作
;再作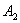 关于
关于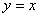 的对称点
的对称点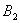 ,将点
,将点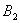 向右水平平移2个单位得到点
向右水平平移2个单位得到点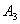 ;….请继续操作并探究:点
;….请继续操作并探究:点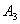 的坐标是 ,点
的坐标是 ,点 的坐标是 .
的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
反比例函数y= 和正比例函数y=mx的部分图象如图所示.
和正比例函数y=mx的部分图象如图所示.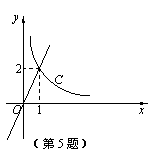 由此可以得到方程
由此可以得到方程 =mx的实数根为
=mx的实数根为
| A.x=1 | B.x=2 |
| C.x1=1,x2=-1 | D.x1=1,x2=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com